
科目:高中物理 来源: 题型:
| an |
| g |
| 1 |
| 3600 |
| 1 |
| 3600 |
| a′ |
| g |
| 1 |
| 3643 |
| 1 |
| 3643 |
查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
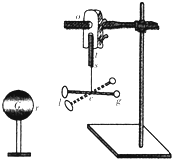 为了验证电荷之间的引力与电荷间距离的平方成反比的规律,库仑还设计了一个电摆实验,其装置如图所示:G为绝缘金属球,lg为虫胶做的小针,悬挂在7~8尺长的蚕丝sc下端,l端放一镀金小圆纸片.G、l间的距离可调.实验时使G、l带异号电荷,则小针受到电引力作用可以在水平面内做小幅摆动.测量出G、l在不同距离时,lg摆动同样次数的时间,从而计算出每次振动的周期.库仑受万有引力定律的启发,把电荷之间的吸引力和地球对物体的吸引力加以类比,猜测电摆振动的周期与带电小纸片l到绝缘带电金属球G之间的距离成正比.库仑记录了三次实验数据如下表: 为了验证电荷之间的引力与电荷间距离的平方成反比的规律,库仑还设计了一个电摆实验,其装置如图所示:G为绝缘金属球,lg为虫胶做的小针,悬挂在7~8尺长的蚕丝sc下端,l端放一镀金小圆纸片.G、l间的距离可调.实验时使G、l带异号电荷,则小针受到电引力作用可以在水平面内做小幅摆动.测量出G、l在不同距离时,lg摆动同样次数的时间,从而计算出每次振动的周期.库仑受万有引力定律的启发,把电荷之间的吸引力和地球对物体的吸引力加以类比,猜测电摆振动的周期与带电小纸片l到绝缘带电金属球G之间的距离成正比.库仑记录了三次实验数据如下表:
(1)根据牛顿万有引力定律和单摆的周期公式可以推断:地面上单摆振动的周期T正比于摆球离开地球表面的距离h. (2)从表格中第1、第2组数据看,电摆的周期与纸片到球心之间的距离可能存在正比例关系. (3)假如电摆的周期与带电纸片到金属球球心距离成正比,则三次测量的周期之比应为20:40:53,但是实验测得值为20:41:60,因此假设不成立. (4)第3组实验测得的周期比预期值偏大,可能是振动时间较长,两带电体漏电造成实验有较大的误差造成的. 则下列选项正确的是( ) |
| A、(2)(4) |
| B、(1)(2)(3)(4) |
| C、(2)(3) |
| D、(1)(3) |
查看答案和解析>>
科目:高中物理 来源:2009年北京市宣武区一模物理试题 题型:058
为了验证电荷之间的引力与电荷间距离的平方成反比的规律,库仑还设计了一个电摆实验,其装置如图所示:G为绝缘金属球,lg为虫胶做的小针,悬挂在7~8尺长的蚕丝sc下端,l端放一镀金小圆纸片.G、l间的距离可调.实验时使G、l带异号电荷,则小针受到电引力作用可以在水平面内做小幅摆动.测量出G、l在不同距离时,lg摆动同样次数的时间,从而计算出每次振动的周期.库仑受万有引力定律的启发,把电荷之间的吸引力和地球对物体的吸引力加以类比,猜测电摆振动的周期与带电小纸片l到绝缘带电金属球G之间的距离成正比.

库仑记录了三次实验数据如下表:

关于本实验及其相关内容,有以下几种说法:
(1)根据牛顿万有引力定律和单摆的周期公式可以推断:地面上单摆振动的周期T正比于摆球离开地球表面的距离h.
(2)从表格中第1、第2组数据看,电摆的周期与纸片到球心之间的距离可能存在正比例关系.
(3)假如电摆的周期与带电纸片到金属球球心距离成正比,则三次测量的周期之比应为20∶40∶53,但是实验测得值为20∶41∶60,因此假设不成立.
(4)第3组实验测得的周期比预期值偏大,可能是振动时间较长,两带电体漏电造成实验有较大的误差造成的.
则下列选项正确的是________
A.(2)(4)
B.(1)(2)(3)(4)
C.(2)(3)
D.(1)(3)
查看答案和解析>>
科目:高中物理 来源:不详 题型:填空题
| an |
| g |
| a′ |
| g |
查看答案和解析>>
科目:高中物理 来源:2011-2012学年浙江省杭州外国语学校高一(下)期中物理试卷(解析版) 题型:填空题
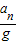 = (用分式表示).
= (用分式表示).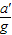 = (用分式表示).
= (用分式表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com