
如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.

(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为 .但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为
.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为 .已知地球和月球的质量分别为
.已知地球和月球的质量分别为 和
和 .求
.求 与
与 两者平方之比.(结果保留3位小数)
两者平方之比.(结果保留3位小数)
(1)  (2)
(2) 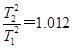
【解析】
试题分析:(1)设两个星球A和B做匀速圆周运动的轨道半径分别为r和R,相互作用的引力大小为F,运行周期为T.根据万有引力定律有
 ①
①
由匀速圆周运动的规律得
 ②
②
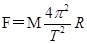 ③
③
由题意得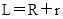 ④
④
联立①②③④式得 .⑤
.⑤
(2)在地月系统中,由于地月系统旋转所围绕的中心O不在地心,月球做圆周运动的周期可由⑤式得出
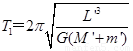 ⑥
⑥
式中,M′和m′分别是地球与月球的质量,L′是地心与月心之间的距离.若认为月球在地球的引力作用下绕地心做匀速圆周运动,则
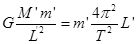 ⑦
⑦
式中,T2为月球绕地心运动的周期.由⑦式得
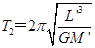 ⑧
⑧
由⑥⑧式得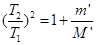
代入题给数据得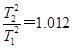 .
.
考点:考查了万有引力定律的应用
点评:关键是对公式的灵活掌握,万有引力这一快的物理公式比较多,注意公式的选择以及变形


科目:高中物理 来源: 题型:
(2010·全国Ⅰ卷)如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为T2.已知地球和月球的质量分别为5.98×1024kg和7.35×1022kg.求T2与T1两者平方之比.(结果保留3位小数)

查看答案和解析>>
科目:高中物理 来源: 题型:
 (注意:在试卷题上作答无效)
(注意:在试卷题上作答无效)
如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。
(1)求两星球做圆周运动的周期:
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为T2。已知地球和月球的质量分别为5.98×1024kg和7.35×1022kg。求T2与T1两者平方之比。(结果保留3位小数)
查看答案和解析>>
科目:高中物理 来源:新人教版高三物理必修2万有引力与航天专项练习(解析版) 题型:计算题
(2010·全国卷1)25.(18分)如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。
求两星球做圆周运动的周期。
在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行为的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期T2。已知地球和月球的质量分别为5.98×1024kg 和 7.35 ×1022kg 。求T2与T1两者平方之比。(结果保留3位小数)

查看答案和解析>>
科目:高中物理 来源:2010年成都七中高一下学期期末考试物理 题型:计算题
(10分)如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。

(1)求两星球做圆周运动的周期:
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为T2。已知地球和月球的质量分别为 和
和 。求T2与T1两者平方之比。(结果保留3位小数)
。求T2与T1两者平方之比。(结果保留3位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com