
分析 两颗恒星都做匀速圆周运动,两颗恒星之间的万有引力提供向心力,根据牛顿第二定律列式求解两星体绕共同圆心做匀速圆周运动的轨道半径之比;
两星体中心距离为r,根据第一问的结论求解出两个半径,然后进一步根据万有引力定律提供向心力列式求解它们共同的角速度.
解答 解:(1)两颗恒星都做匀速圆周运动,两颗恒星之间的万有引力提供向心力,根据牛顿第二定律,有:
对m1:$G\frac{{m}_{1}{m}_{2}}{{r}^{2}}={m}_{1}{ω}^{2}{r}_{1}$ ①
对m2:$G\frac{{m}_{1}{m}_{2}}{{r}^{2}}={m}_{2}{ω}^{2}{r}_{2}$ ②
故:m1r1=m2r2
r1:r2=m2:m1 ③
(2)由于r1+r2=r,结合③式解得:
r1=$\frac{{m}_{2}r}{{m}_{1}+{m}_{2}}$ ④
将④式代入①式,解得:
ω=$\sqrt{\frac{G({m}_{1}+{m}_{2})}{{r}^{3}}}$
故答案为:m2:m1; $\sqrt{\frac{G({m}_{1}+{m}_{2})}{{r}^{3}}}$.
点评 本题是双星问题,与卫星绕地球运动模型不同,两颗星都绕同一圆心做匀速圆周运动,关键抓住条件:角速度相同.


科目:高中物理 来源: 题型:解答题
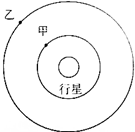 甲、乙两颗卫星绕同一行星做圆周运动,运动方向相同,如图所示,卫星甲的周期为T1,卫星行星乙的周期为T2.若T2>T1,在某一时刻t0两颗卫星相遇(两卫星距离最近),问:
甲、乙两颗卫星绕同一行星做圆周运动,运动方向相同,如图所示,卫星甲的周期为T1,卫星行星乙的周期为T2.若T2>T1,在某一时刻t0两颗卫星相遇(两卫星距离最近),问:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 直角三角形金属框abc放置在竖直向上的匀强磁场中,磁感应强度大小为B,方向平行于ab边向上,若金属框绕ab边向纸面外以角速度ω匀速转动90°(从上往下看逆时针转动),如图甲所示,c、a两点的电势差为Uca,通过ab边的电荷量为q,若金属框绕bc边向纸面内以角速度ω匀速转动90°,如图乙所示,c、a两点的电势差为Uca′,通过ab边的电荷量为q′,已知bc、ab边的长度都为l,金属框的总电阻为R,下列判断正确的是( )
直角三角形金属框abc放置在竖直向上的匀强磁场中,磁感应强度大小为B,方向平行于ab边向上,若金属框绕ab边向纸面外以角速度ω匀速转动90°(从上往下看逆时针转动),如图甲所示,c、a两点的电势差为Uca,通过ab边的电荷量为q,若金属框绕bc边向纸面内以角速度ω匀速转动90°,如图乙所示,c、a两点的电势差为Uca′,通过ab边的电荷量为q′,已知bc、ab边的长度都为l,金属框的总电阻为R,下列判断正确的是( )| A. | Uca=$\frac{1}{2}$Bωl2 | B. | Uca′=$\frac{1}{2}$Bωl2 | C. | q=$\frac{\sqrt{2}Bπ{l}^{2}}{8R}$ | D. | q′=$\frac{B{l}^{2}}{2R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
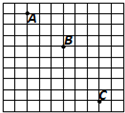 在“研究小球做平抛运动”的实验中:
在“研究小球做平抛运动”的实验中:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | F1=5N,F2=5N,F3=1N | B. | F1=1N,F2=3N,F3=1N | ||
| C. | F1=2N,F2=4N,F3=6N | D. | F1=6N,F2=10N,F3=8N |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
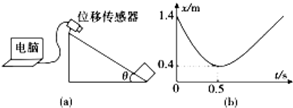
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
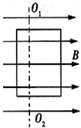 (多选)在匀强磁场中匀速转动的矩形线圈的周期为T,转轴01O2垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么( )
(多选)在匀强磁场中匀速转动的矩形线圈的周期为T,转轴01O2垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么( )| A. | 线圈中感应电流的有效值为2A | |
| B. | 线圈消耗的电功率为4W | |
| C. | 任意时刻线圈中的感应电动势为e=4cos$\frac{2π}{T}$t | |
| D. | 任意时刻穿过线圈的磁通量为Φ=$\frac{T}{π}$sin$\frac{2π}{T}$t |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com