火星是近年太空探索的一个热点,也许将来的某一天,你会乘坐火星车在火星表面游览.设火星的质量为M,半径为R,万有引力常量为G,且火星车可视为质点.在与水平面成θ角的平整斜坡上,一火星车制动后,以初速度υ0向上能滑行的最大距离为s.那么,车与斜坡间的动摩擦因数应该等于多少?
解:以火星车为研究对象,进行受力分析.如图所示
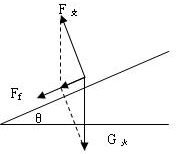
火星车受到的摩擦力 F
f=μF
N (1)
火星车受到的支持力 F
N=mg
火cosθ (2)
在火星表面,重力等于引力,则有mg
火=
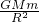
(3)
沿斜面向车与斜坡间的动摩擦因数应该等于上的减速运动可看成沿斜面向下的加速运动
则由运动学公式,则有v
2=2as (4)
在斜面方向上,由牛顿第二定律得
mg
火sinθ+F
f=ma (5)
由(1)-(5)式可解得
μ=
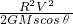
-tanθ
即车与斜坡间的动摩擦因数应该等于
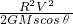
-tanθ.
分析:运用火星车在火星表面的重力与引力关系,求火星表面的重力加速度;再运动学公式求出火星车在斜面上的加速度;最后利用牛顿第二定律列出重力加速度、车的加速度与摩擦因数关系.
点评:让学生掌握万有引力定律、牛顿运动定律及匀变速直线运动规律,同时培养学生提高分析与解决问题能力.


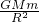 (3)
(3)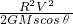 -tanθ
-tanθ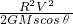 -tanθ.
-tanθ.
