
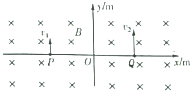
 如图所示的平面直角坐标系内分布有足够大的匀强磁场,磁感应强度B=0.05T,方向垂直纸面向里,x轴上相距为L=0.12m的P、Q两点关于原点对称,两点处均有一个粒子发射器(发射一个粒子后即移开),能分别在纸面内沿y轴正方向发射带电粒子,已知P点发射的粒子带负电,速率为v1=3.0×104m/s,Q点发射的粒子带正电,粒子的比荷均为$\frac{q}{m}$=2.0×107C/kg,Q处的粒子先发射,P处的粒子后发射,发射的时间差为△t=$\frac{16π}{180}$×10-6s,已知P处发射的粒子运动t=$\frac{127π}{180}$×10-6s时间后,恰与Q处发射的粒子在第二象限内相遇,不计粒子的重力和粒子之间的相互作用力.
如图所示的平面直角坐标系内分布有足够大的匀强磁场,磁感应强度B=0.05T,方向垂直纸面向里,x轴上相距为L=0.12m的P、Q两点关于原点对称,两点处均有一个粒子发射器(发射一个粒子后即移开),能分别在纸面内沿y轴正方向发射带电粒子,已知P点发射的粒子带负电,速率为v1=3.0×104m/s,Q点发射的粒子带正电,粒子的比荷均为$\frac{q}{m}$=2.0×107C/kg,Q处的粒子先发射,P处的粒子后发射,发射的时间差为△t=$\frac{16π}{180}$×10-6s,已知P处发射的粒子运动t=$\frac{127π}{180}$×10-6s时间后,恰与Q处发射的粒子在第二象限内相遇,不计粒子的重力和粒子之间的相互作用力.分析 (1)根据洛仑兹力充当向心力可明确粒子半径;再求得转动周期;根据题意即可明确相遇时转过的角度,则可明确相遇点的坐标;
(2)根据几何关系可求得Q处粒子的半径,再由洛仑兹力充当向心力即可求得粒子速率;
(3)根据题意明确如何才能使两粒子不会相遇,再由洛仑兹力充当向心力即可求得粒子速率.
解答 解:(1)由洛仑兹力充当向心力可得:
Bqv=m$\frac{{v}^{2}}{R}$
P粒子半径为:RP=$\frac{mv}{Bq}$=$\frac{3×1{0}^{4}}{0.05}$×$\frac{1}{2×1{0}^{7}}$=0.03m;
周期为:T=$\frac{2πm}{Bq}$=$\frac{2π}{0.05}×\frac{1}{1.0×1{0}^{7}}$=2π×10-6s
经t=$\frac{127π}{180}$×10-6s后,转动周期数为:n=$\frac{\frac{127π}{180}}{2π}$=$\frac{127}{360}$T;
故说明P粒子转动127度后与Q粒子相遇;由几何关系可知;交点竖直方向运动位移为:y=Rsin53°=0.03×0.8cm=0.024m;
水平方向离圆心的距离为:x=Rcos53°=0.03×0.6=0.018cm;
则x方向离O点距离为:0.03-0.018=0.012m
故坐标为:(-0.012,0.024)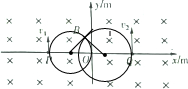 (2)由几何关系可知,Q粒子的半径有:R′+R′cos37°=0.06+0.012
(2)由几何关系可知,Q粒子的半径有:R′+R′cos37°=0.06+0.012
解得:R′=0.04m;
则由Bqv=m$\frac{{v}^{2}}{R}$
v2=$\frac{BqR}{m}$=0.05×0.04×2.0×107=4×104m/s;
(3)根据题意可知,要使两粒子无论怎样取时间差值,都不能相遇; 若速度较小,则两圆外切,若速度较大,则两圆内切;
则Q粒子的半径应大于等于0.06m或小于等于0.03m;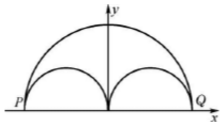
则可得:v2<$\frac{BqR}{m}$=0.05×0.03×2.0×107=3×104m/s或
v2>$\frac{BqR}{m}$=0.05×0.06×2.0×107=6×104m/s;
答:(1)求两粒子相遇点S(图中未画出)的坐标为(-0.012,0.024)
(2)求Q处发射粒子的速率v2为4×104m/s
(3)P处发射粒子后,调节Q处发射粒子速率v2的值,发现不管△t取何值,两粒子总不能相遇,这种情形下v2的值应大于等于6×104m/s或小于等于3×104m/s
点评 本题属于带电粒子在磁场中的运动问题,里面涉及两个粒子的运动情况;从而增大了难度;但是只要明确洛仑兹力充当向心力及几何关系的正确应用,通过认真分析是可以顺利求解的.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
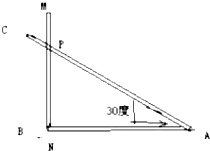 如图所示,棒MN在夹角为30度的导轨BAC上向左滑行,若再滑行过程中棒始终垂直于AB边,且速度为1.2m/s,那么MN与AC的交点P沿AC导轨滑行速度是0.8$\sqrt{3}$m/s.
如图所示,棒MN在夹角为30度的导轨BAC上向左滑行,若再滑行过程中棒始终垂直于AB边,且速度为1.2m/s,那么MN与AC的交点P沿AC导轨滑行速度是0.8$\sqrt{3}$m/s.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 同一物体在地球(视为均匀球体)上的任何位置所受重力都相等 | |
| B. | 同一物体在地球(视为均匀球体)上的任何位置所受万有引力的大小都相等 | |
| C. | 开普勒指出所有行星都在同一平面内以太阳为公共焦点的椭圆轨道上运动 | |
| D. | 牛顿发现万有引力定律并通过扭秤实验测出引力常量 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
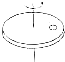 如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动,关于这种情况下硬币的受力情况,下列说法正确的是( )
如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动,关于这种情况下硬币的受力情况,下列说法正确的是( )| A. | 只受重力和台面的支持力 | |
| B. | 受重力、台面的支持力和向心力 | |
| C. | 受重力、台面的支持力和静摩擦力 | |
| D. | 受重力、台面的支持力、向心力和静摩擦力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 3g | B. | 16g | C. | $\frac{1}{9}g$ | D. | $\frac{1}{16}g$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 椭圆的一个焦点上 | B. | 椭圆的两个焦点连线的中点上 | ||
| C. | 椭圆轨迹上的一点 | D. | 任意一点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com