分析:(1)带电小球进入复合场做匀速圆周运动,重力与电场力平衡,可得到场强.小球在t=
T时刻进入复合场,与物块碰后做匀速圆周运动,恰能垂直于边界GH返回低一级平台上,返回低一级台阶的过程,磁场方向与小球进入复合场时磁场方向相反,说明小球从高一级平台进入复合场到与物块碰撞经过的时间等于
,由小球做匀速圆周运动的周期公式T′=
即可求出交变磁场变化的周期T;
(2)小球在复合场中由洛伦兹力提供向心力,根据牛顿第二定律求解小球从高一级平台左边缘滑出的初速度v;
(3)小球与绝缘板的碰撞是弹性碰撞,系统动量守恒,机械能也守恒,根据守恒定律列方程后联立求解即可;
(4)根据牛顿第二定律求出小球与物块碰后的速率,根据能量守恒求出物块获得的动能,并由能量守恒求解绝缘物块从C点运动至D点时,弹簧具有的弹性势能E
p.
解答:解:(1)带电小球垂直于边界GH进入复合场,运动到O点恰与绝缘板碰撞,碰后能返回平台,说明小球在复合场中qE=mg--------①
洛仑兹力做匀速圆周运动的向心力,且经过半个圆周到达O点,碰后再经过半个周期回到二级平台.
根据带电粒子在磁场运动的周期公式 T=
------------------------②
①②消去q,得交变磁场变化的周期 T=
--------------------------
(2)由牛顿第二定律有:qvB=m
------------------------------③
由几何关系有:r=
h----------------------------------④
①③④联立,解得:v=
-----------------------------------⑤
(3)设小球碰撞后的速度大小为V,绝缘板的速度大小为V
m.则题意可知,小球返回的半径r′=
=
,又根据r=
可得:则V=
--------⑥
小球与绝缘板碰撞过程中,以小球和绝缘板为系统,动量守恒.
有:mv=-mV+MV
m------------------------------------⑦
而小球与绝缘板发生的是弹性碰撞,它们构成的系统机械能守恒,有:
有:
mv
2=
mV
2+
MV
m2--------------------------------⑧
⑤⑥⑦联立解得:M=3m----------------------------------------⑨
(4)绝缘板从C点运动至D点的过程中,根据功能关系有:
E
P+μMgS=
MV
m2------------------------------------⑩
①③⑤⑥⑦⑨⑩联立解得:E
P=
-3μmgS
答:(1)交变磁场变化的周期T为
;
(2)小球从高一级平台左边缘滑上的初速度v为
;
(3)绝缘板的质量M为3m;
(4)绝缘板从C点运动至D点时,弹簧具有的弹性势能为
-3μmgS.




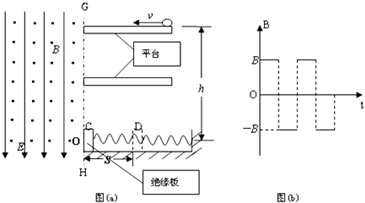


![]()
