Question

(20分) 两颗人造卫星绕地球沿同一椭圆轨道同向运动，它们通过轨道上同一点的时间相差半个周期．已知轨道近地点离地心的距离是地球半径R的2倍，卫星通过近地点时的速度，式中M为地球质量，G为引力常量．卫星上装有同样的角度测量仪，可测出卫星与任意两点的两条连线之间的夹角．试设计一种测量方案，利用这两个测量仪测定太空中某星体与地心在某时刻的距离．（最后结果要求用测得量和地球半径R表示）

Answer 1

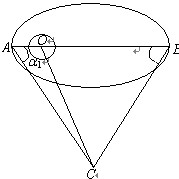
如图，卫星绕地球运动的轨道为一椭圆，地心位于轨道椭圆的一个焦点O处，设待测量星体位于C处．根据题意，当一个卫星运动到轨道的近地点A时，另一个卫星恰好到达远地点B处，只要位于A点的卫星用角度测量仪测出AO和AC的夹角α₁，位于B点的卫星用角度测量仪测出BO和BC的夹角α₂，就可以计算出此时星体C与地心的距离OC．

因卫星椭圆轨道长轴的长度

                (1)

式中r_近、与r_远分别表示轨道近地点和远地点到地心的距离．由角动量守恒

              (2)

式中m为卫星的质量．由机械能守恒

     (3)

已知

，      

得                (4)

所以                (5)

在△ABC中用正弦定理

               (6)

所以                (7)

地心与星体之间的距离为，在△BOC中用余弦定理

               (8)

由式(4)、(5)、(7)得

               

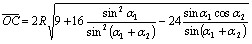               (9)

评分标准：

本题20分．(1)式2分，(2)、(3)式各3分，(6) 、(8)式各3分， (9) 式6分．