
分析 根据洛伦兹力提供向心力得出线速度、周期与轨道半径的表达式,从而得出速度大小之比和周期之比,结合速度之比求出动能之比.
解答 解:(1)根据$k\frac{{e}^{2}}{{r}^{2}}=m\frac{{v}^{2}}{r}$得,v=$\sqrt{\frac{k{e}^{2}}{mr}}$,.
(2)根据$k\frac{{e}^{2}}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,T=$\sqrt{\frac{4{π}^{2}m{r}^{3}}{k{e}^{2}}}$,
因为轨道半径之比为1:4,则周期之比为1:8.
(3)根据$k\frac{{e}^{2}}{{r}^{2}}=m\frac{{v}^{2}}{r}$得,动能${E}_{k}=\frac{1}{2}m{v}^{2}=\frac{1}{2}•\frac{k{e}^{2}}{r}$,
因为轨道半径之比为1:4,则动能之比为4:1.
答:(1)电子在距离原子核r的圆轨道上做匀速圆周运动的速度大小为$\sqrt{\frac{k{e}^{2}}{mr}}$;
(2)电子在距离原子核r和4r的圆轨道上做匀速圆周运动的周期之比为1:8;
(3)电子在距离原子核r和4r的圆轨道上做匀速圆周运动的动能之比为4:1.
点评 解决本题的关键知道电子做圆周运动向心力的来源,结合牛顿第二定律进行求解,难度不大.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 2010年10月1日,中国探月二期工程先导星“嫦娥二号”在西昌点火升空,准确入轨,赴月球拍摄月球表面影像、获取极区表面数据,如图所示,假设在地月转移轨道上运动时处于无动力状态,已知地球的质量为月球质量的81倍,当卫星进入地月转移轨道中速度最小时,它与月球中心和地球中心的距离之比为( )
2010年10月1日,中国探月二期工程先导星“嫦娥二号”在西昌点火升空,准确入轨,赴月球拍摄月球表面影像、获取极区表面数据,如图所示,假设在地月转移轨道上运动时处于无动力状态,已知地球的质量为月球质量的81倍,当卫星进入地月转移轨道中速度最小时,它与月球中心和地球中心的距离之比为( )| A. | 1:3 | B. | 1:9 | C. | 1:27 | D. | 9:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两块平行金属板M,N水平放置,两板间距为a,充电后板间有匀强电场E,一个质量为m,带电量为e的质子在M板附近由静止释放,则质子到达N板时速度有多大?(不计重力)
如图所示,两块平行金属板M,N水平放置,两板间距为a,充电后板间有匀强电场E,一个质量为m,带电量为e的质子在M板附近由静止释放,则质子到达N板时速度有多大?(不计重力)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 该质点总的运动是自由落体运动和圆周运动的叠加 | |
| B. | 该质点在磁场区域中所受的合力是一个恒力 | |
| C. | 该质点在磁场区域中所受的合力是一个大小不变,方向改变的力 | |
| D. | 该质点在磁场区域中所受的合力是重力和洛仑兹力的合力 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,竖直放置的光滑圆环上,穿过一个绝缘小球,小球质量为m,带电量为q,整个装置置于水平向左的匀强电场中.今将小球从与环心O在同一水平线上的A点由静止释放,它刚能顺时针方向运动到环的最高点D,而速度为零,已知圆环半径为r,重力加速度为g.则
如图所示,竖直放置的光滑圆环上,穿过一个绝缘小球,小球质量为m,带电量为q,整个装置置于水平向左的匀强电场中.今将小球从与环心O在同一水平线上的A点由静止释放,它刚能顺时针方向运动到环的最高点D,而速度为零,已知圆环半径为r,重力加速度为g.则查看答案和解析>>
科目:高中物理 来源: 题型:选择题
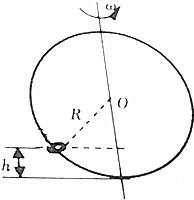 如图所示,半径为R的光滑大环上套有一个质量为m的小环,当大环以角速度ω绕着通过环心O的竖直轴旋转时,要使小环随大环在一定高度h(h>0)处做水平匀速圆周运动.则角速度ω的取值应满足( )
如图所示,半径为R的光滑大环上套有一个质量为m的小环,当大环以角速度ω绕着通过环心O的竖直轴旋转时,要使小环随大环在一定高度h(h>0)处做水平匀速圆周运动.则角速度ω的取值应满足( )| A. | ω>0 | B. | ω>$\sqrt{\frac{g}{R}}$ | C. | ω<$\sqrt{\frac{g}{R}}$ | D. | ω=$\sqrt{\frac{g}{R}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com