
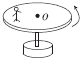
 在快乐向前冲娱乐节目中有一关为疯狂大转盘,图示为其简化模型,圆盘绕轴匀速转动时,在到圆心O的距离R=0.8m处有一质量m=50kg的人恰好能随圆盘做匀速圆周运动而不被甩出,此时圆盘的角速度ω=2rad/s.(人视为质点)
在快乐向前冲娱乐节目中有一关为疯狂大转盘,图示为其简化模型,圆盘绕轴匀速转动时,在到圆心O的距离R=0.8m处有一质量m=50kg的人恰好能随圆盘做匀速圆周运动而不被甩出,此时圆盘的角速度ω=2rad/s.(人视为质点)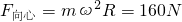
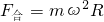 可知,
可知,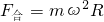 可知,人随圆盘做圆周运动需要的向心力越大,圆盘对人的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以人不能随圆盘做匀速圆周运动.
可知,人随圆盘做圆周运动需要的向心力越大,圆盘对人的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以人不能随圆盘做匀速圆周运动.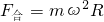 可知,人随圆盘做圆周运动需要的向心力越大,而圆盘对人的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以人不能随圆盘做匀速圆周运动.
可知,人随圆盘做圆周运动需要的向心力越大,而圆盘对人的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以人不能随圆盘做匀速圆周运动.

 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
 (2012?山西二模)在快乐向前冲娱乐节目中有一关为疯狂大转盘,图示为其简化模型,圆盘绕轴匀速转动时,在到圆心O的距离R=0.8m处有一质量m=50kg的人恰好能随圆盘做匀速圆周运动而不被甩出,此时圆盘的角速度ω=2rad/s.(人视为质点)
(2012?山西二模)在快乐向前冲娱乐节目中有一关为疯狂大转盘,图示为其简化模型,圆盘绕轴匀速转动时,在到圆心O的距离R=0.8m处有一质量m=50kg的人恰好能随圆盘做匀速圆周运动而不被甩出,此时圆盘的角速度ω=2rad/s.(人视为质点)查看答案和解析>>
科目:高中物理 来源:2012年山西省高考物理二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com