
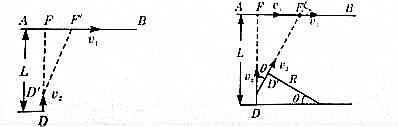
分析 (1)猎犬的运动方向始终对准狐狸且速度大小不变,故猎犬做匀速率曲线运动,根据向心加速度a=$\frac{{v}_{2}^{2}}{r}$,r为猎犬所在处的曲率半径,因为r不断变化,故猎犬的加速度的大小、方向都在不断变化,题目要求猎犬在D处的加速度大小,由于v2大小不变,如果求出D点的曲率半径,此时猎犬的加速度大小也就求得了;
(2)根据速度的合成与分解,结合数学知识求时间.
解答  解:(1)猎犬做匀速率曲线运动,其加速度的大小和方向都在不断改变.在所求时刻开始的一段很短的时间内,猎犬运动的轨迹可近似看做是一段圆弧,设其半径为R,
解:(1)猎犬做匀速率曲线运动,其加速度的大小和方向都在不断改变.在所求时刻开始的一段很短的时间内,猎犬运动的轨迹可近似看做是一段圆弧,设其半径为R,
则加速度a=$\frac{{v}_{2}^{2}}{R}$,
其方向与速度方向垂直,如图所示.在极短时间△t内,设狐狸与猎犬分别到达F′与D′,
猎犬的速度方向转过的角度为:θ=$\frac{{v}_{2}t}{R}$,tanα=$\frac{{v}_{1}t}{L}$,
由于时间极短,α角很小,则有:tanα≈α,且α≈θ
则得:$\frac{{v}_{2}t}{R}$=$\frac{{v}_{1}t}{L}$解得:R=$\frac{L{v}_{2}}{{v}_{1}}$
所以猎犬的加速度大小为a=$\frac{{v}_{2}^{2}}{R}$=$\frac{{v}_{2}^{2}}{\frac{L{v}_{2}}{{v}_{1}}}$=$\frac{{v}_{1}{v}_{2}}{L}$
(2)如上图所示:$\frac{{v}_{1}}{{v}_{2}}$=sinθ
t=$\frac{L}{cosθ}$,cosθ=$\sqrt{1-si{n}^{2}θ}$
解得:t=$\frac{L}{{v}_{2}\sqrt{1-\frac{{v}_{1}^{2}}{{v}_{2}^{2}}}}$=$\frac{L}{\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}}$.
答:(1)此时猎犬的加速度的大小$\frac{{v}_{1}{v}_{2}}{L}$;
(2)猎犬追上狐狸需要的时间为$\frac{L}{\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}}$.
点评 本题采用微元法研究猎犬的加速度.要知道当α很小时常取sinα=tanα=α,这在微元法解题中是常运用的等式.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中物理 来源: 题型:选择题
| A. | $\frac{p}{t}$ | B. | $\frac{p}{273}$ | C. | $\frac{{p-{p_0}}}{t}$ | D. | $\frac{p_0}{t+273}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0做平抛运动,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动.则下列说法错误的是( )
甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0做平抛运动,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动.则下列说法错误的是( )| A. | 若甲、乙、丙三球同时相遇,则一定发生在P点 | |
| B. | 若甲、丙二球在空中相遇,此时乙球一定在P点 | |
| C. | 若甲与丙距离足够大,则丙球一定先落地 | |
| D. | 任意时刻甲、乙的水平位移一定相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 质量为m的物体悬挂在轻质的且各结点A、B、C采用胶链连接的支架上,斜梁OB与竖直方向的夹角为θ.设水平横梁OA和斜梁OB作用与O点的弹力分别为FA和FB,试采用力的分解或力的合成的方法求FA和FB的大小和方向.(选用任一种方法均可) (已知重力加速度为g )
质量为m的物体悬挂在轻质的且各结点A、B、C采用胶链连接的支架上,斜梁OB与竖直方向的夹角为θ.设水平横梁OA和斜梁OB作用与O点的弹力分别为FA和FB,试采用力的分解或力的合成的方法求FA和FB的大小和方向.(选用任一种方法均可) (已知重力加速度为g )查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{1}{2}$R | B. | $\frac{\sqrt{2}}{2}$R | C. | $\sqrt{2}$R | D. | 2R |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
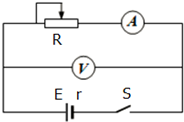 如图所示为测干电池的电动势和内阻的电路图,用两节干电池串联作为电源(每节电池电动势接近1.5V,内阻约为0.5Ω),除给出的电源、导线和开关外,还有以下器材:
如图所示为测干电池的电动势和内阻的电路图,用两节干电池串联作为电源(每节电池电动势接近1.5V,内阻约为0.5Ω),除给出的电源、导线和开关外,还有以下器材:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 链球运动员将链球旋转后抛出 | |
| B. | 人沿直线跑步时突然跌倒 | |
| C. | 圆柱上的细绳系一小球,小球绕圆柱转动使细绳缠绕在圆柱上 | |
| D. | 铅球运动员将铅球抛出 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com