
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中物理 来源: 题型:
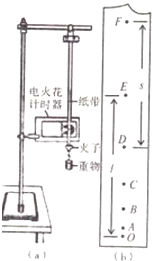 使用如图(a)所示的装置验证机械能守恒定律,打出一条纸带如图(b)所示,O是打出的第一个点迹,A、B、C、D、E、F…是依次打出的点迹,量出OE间的距离为L,DF间的距离为s.已知打点计时器打点的周期是T,当地的重力加速度为g.
使用如图(a)所示的装置验证机械能守恒定律,打出一条纸带如图(b)所示,O是打出的第一个点迹,A、B、C、D、E、F…是依次打出的点迹,量出OE间的距离为L,DF间的距离为s.已知打点计时器打点的周期是T,当地的重力加速度为g.| 1 |
| 8 |
| S |
| T |
| 1 |
| 8 |
| S |
| T |
| 1 |
| 8 |
| S |
| T |
| 1 |
| 8 |
| S |
| T |
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源:广东 题型:问答题
查看答案和解析>>
科目:高中物理 来源:2012年广东省高考物理试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com