
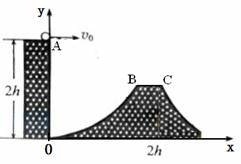
(2013上海奉贤区测试)一探险队在探险时遇到一山沟,山沟的一侧OA竖直,另一侧的坡面OB呈抛物线形状,与一平台BC相连,如图所示。已知山沟竖直一侧OA的高度为2h,平台离沟底h高处,C点离竖直OA的水平距离为2h。以沟底的O点为原点建立坐标系xOy,坡面的抛物线方程为y=x2/2h。质量为m的探险队员从山沟的竖直一侧,沿水平方向跳向平台。人视为质点,忽略空气阻力,重力加速度为g。求:
(1)若探险队员以速度v0水平跳出时,掉在坡面OB的某处,则他在空中运动的时间为多少?
(2)为了能跳在平台上,他的初速度应满足什么条件?请计算说明。
(3)若已知探险队员水平跳出,刚到达OBC面的动能Ek=1.55mgh,则他跳出时的水平速度可能为多大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com