
 如图所示,半径为r的圆形匀强磁场区域I与x轴相切与坐标系的原点O,磁感应强度为B1,方向垂直于纸面向外,磁场区域I右侧有一长方体加速管,加速管底面宽度为2r,轴线与x轴平行且过磁场区域I的圆心,左侧的电势比右侧高U.在加速管出口下侧距离2r处放置一宽度为2r的荧光屏,加速管右侧存在方向垂直于纸面向外的匀强磁场区域II,在O点处有一个粒子源,能沿纸面向y>0的各个方向均匀地发射大量质量为m、带电荷量为q且速率相同的粒子,其中沿y轴正方向射入磁场的粒子,恰能沿轴线进入长方形加速管并打在荧光屏的中心位置,(不计粒子重力及其相互作用)
如图所示,半径为r的圆形匀强磁场区域I与x轴相切与坐标系的原点O,磁感应强度为B1,方向垂直于纸面向外,磁场区域I右侧有一长方体加速管,加速管底面宽度为2r,轴线与x轴平行且过磁场区域I的圆心,左侧的电势比右侧高U.在加速管出口下侧距离2r处放置一宽度为2r的荧光屏,加速管右侧存在方向垂直于纸面向外的匀强磁场区域II,在O点处有一个粒子源,能沿纸面向y>0的各个方向均匀地发射大量质量为m、带电荷量为q且速率相同的粒子,其中沿y轴正方向射入磁场的粒子,恰能沿轴线进入长方形加速管并打在荧光屏的中心位置,(不计粒子重力及其相互作用)分析 (1)由运动方向通过几何关系求得半径,进而由洛伦兹力作向心力求得速度;
(2)应用动能定理取得进入磁场的粒子速度,再由几何关系求得半径,由洛伦兹力作向心力联立两式求得磁感应强度;
(3)先通过几何关系求得粒子在加速管中的分布,然后由粒子运动的半径及几何关系求得可打在荧光屏上的粒子范围,进而求得数目.
解答 解:(1)沿y轴正方向射入磁场的粒子,恰能沿轴线进入长方形加速管并打在荧光屏的中心位置,则磁场区域I内粒子运动轨迹半径距离为r,
在匀强磁场Ⅰ中粒子做圆周运动,洛伦兹力作向心力,则有:${B}_{1}vq=\frac{m{v}^{2}}{r}$,
解得:$v=\frac{{B}_{1}qr}{m}$;
(2)沿y轴正方向射入磁场的粒子,恰能沿轴线进入长方形加速管,则由动能定理可得粒子进入磁场Ⅱ的速度为v′,有关系式:$Uq=\frac{1}{2}mv{′}^{2}-\frac{1}{2}m{v}^{2}$;
解得:$v′=\sqrt{\frac{2Uq}{m}+{v}^{2}}$;
因为粒子在磁场Ⅱ中运动,并打在荧光屏的中心位置,所以,粒子在磁场Ⅱ中做圆周运动的半径R′=2r,
由洛伦兹力作向心力可得:${B}_{2}v′q=\frac{mv{′}^{2}}{R′}$,所以,${B}_{2}=\frac{mv′}{qR′}=\frac{m\sqrt{\frac{2Uq}{m}+{v}^{2}}}{2qr}$,其中$v=\frac{{B}_{1}qr}{m}$;
(3)在匀强磁场Ⅰ中,设粒子从P点离开磁场,如图所示, ,
,
因为粒子做圆周运动的圆心在弦长的垂直平分线上,且磁场区域和圆周运动的半径都为r,所以,磁场区域的两条半径和圆周运动轨迹的两条半径构成菱形,所以,在P点的径向平行于y轴,所以,粒子离开磁场时的速度为水平方向.
若进入加速管的粒子数目为N,则这N个粒子在竖直方向上均匀分布;
在磁场中粒子做匀速圆周运动,洛伦兹力作向心力,有:$Bvq=\frac{m{v}^{2}}{R}$,
解得:$R=\frac{mv}{Bq}$;
磁场II的磁感应强度B2减小10%时,则粒子在磁场Ⅱ中做圆周运动的半径为:$R″=\frac{R′}{90%}=\frac{20}{9}r$,
设粒子进入磁场Ⅱ时,竖直高度为y,则只要:0≤2R″-2r-y≤2r,粒子就可以打在荧光屏上,
所以,$\frac{4}{9}r≤y≤\frac{22}{9}r$,因为N个粒子在0≤y≤2r上均匀分布,所以打在屏上的粒子数为:$n=\frac{2r-\frac{4}{9}r}{2r}N=\frac{7}{9}N$.
答:(1)粒子刚进入加速管时的速度大小为$\frac{{B}_{1}qr}{m}$;
(2)磁场区域II的磁感应强度大小B2为$\frac{m\sqrt{\frac{2Uq}{m}+{v}^{2}}}{2qr}$,其中$v=\frac{{B}_{1}qr}{m}$;
(3)若进入加速管的粒子数目为N,则磁场II的磁感应强度B2减小10%时,有$\frac{7}{9}N$个离子能打在荧光屏上.
点评 求解粒子在匀强磁场中的运动问题时,应用几何关系要注意数量关系,如本题在磁场Ⅰ中,半径都是r,才能形成菱形,得到出射速度方向.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:计算题
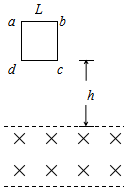 均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m.将其置于磁感应强度为B的水平匀强磁场上方h处,如图所示.线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界平行.当cd边刚进入磁场时:
均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m.将其置于磁感应强度为B的水平匀强磁场上方h处,如图所示.线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界平行.当cd边刚进入磁场时:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
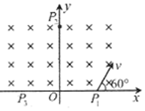 如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,一个带电粒子X第一次从x轴上的P1点以一定的速度进入磁场,已知粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成60°角,粒子穿过y轴正半轴的P2点时方向沿-x方向,粒子X从x轴上的P3点离开磁场,该带电粒子X第二次以相同的速度仍从P1点进入磁场,经过P2点时与一个静止的不带电的粒子Y发生正碰并立即结合为一个整体Z继续运动,离开磁场时经过x轴上的P4点,已知粒子X和粒子Y质量均为m,两个粒子的重力均不计,求:
如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,一个带电粒子X第一次从x轴上的P1点以一定的速度进入磁场,已知粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成60°角,粒子穿过y轴正半轴的P2点时方向沿-x方向,粒子X从x轴上的P3点离开磁场,该带电粒子X第二次以相同的速度仍从P1点进入磁场,经过P2点时与一个静止的不带电的粒子Y发生正碰并立即结合为一个整体Z继续运动,离开磁场时经过x轴上的P4点,已知粒子X和粒子Y质量均为m,两个粒子的重力均不计,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | v=ωR、ω=2πT | B. | v=ωR、a=2Rω | C. | ω=Rv、ωT=2π | D. | v=$\frac{2πR}{T}$、a=vω |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 小船渡河的最短时间为20s | |
| B. | 要使小船渡河的位移最短,则船身与河岸上游应垂直 | |
| C. | 船渡河的最小位移为100m | |
| D. | 船渡河的最小位移为125m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 现代质谱仪可用来分析比质子重很多的离子,其示意图如图所示,其中加速电压恒定.质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场.若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍.则关于离子和质子的质量比正确的是( )
现代质谱仪可用来分析比质子重很多的离子,其示意图如图所示,其中加速电压恒定.质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场.若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍.则关于离子和质子的质量比正确的是( )| A. | 11 | B. | 12 | C. | 144 | D. | 121 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
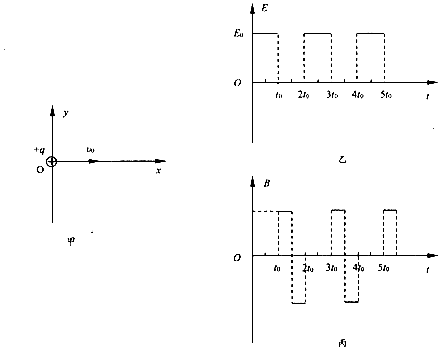 在如图甲所示的xOy平面内,y轴右侧空间有分布均匀、大小随时间周期性变化的电场和磁场,其变化规律分别如图乙、丙所示,电场强度大小为E0,方向沿y轴负方向,垂直xOy平面向里为磁场的正方向.在t=0时刻,质量为m、电荷量为+q的粒子,以初速度大小为υ0从坐标原点O沿x轴正方向出发,已知粒子在磁场中做圆周运动的周期为t0,不计粒子的重力,求粒子在:
在如图甲所示的xOy平面内,y轴右侧空间有分布均匀、大小随时间周期性变化的电场和磁场,其变化规律分别如图乙、丙所示,电场强度大小为E0,方向沿y轴负方向,垂直xOy平面向里为磁场的正方向.在t=0时刻,质量为m、电荷量为+q的粒子,以初速度大小为υ0从坐标原点O沿x轴正方向出发,已知粒子在磁场中做圆周运动的周期为t0,不计粒子的重力,求粒子在:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
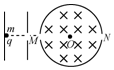 一圆筒的横截面如图所示,圆心为O、半径为R,在筒上有两个小孔M,N且M、O、N在同一水平线上.圆筒所在区域有垂直于圆筒截面的匀强磁场,磁感应强度大小为B,在圆筒左侧有一个加速电场.一个质量为m、电荷量为q的带正电粒子,由静止经电场加速后从M孔沿MO方向射入圆筒.已知粒子与圆筒碰撞时电荷量保持不变,碰撞后速度大小不变,方向与碰撞前相反,不计粒子重力.
一圆筒的横截面如图所示,圆心为O、半径为R,在筒上有两个小孔M,N且M、O、N在同一水平线上.圆筒所在区域有垂直于圆筒截面的匀强磁场,磁感应强度大小为B,在圆筒左侧有一个加速电场.一个质量为m、电荷量为q的带正电粒子,由静止经电场加速后从M孔沿MO方向射入圆筒.已知粒子与圆筒碰撞时电荷量保持不变,碰撞后速度大小不变,方向与碰撞前相反,不计粒子重力.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 它们的运行周期都是24小时 | B. | 它们的到地球表面的距离是确定的 | ||
| C. | 它们都以7.9km/s做圆周运动 | D. | 它们做圆周运动的圆心是地心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com