救护车在平直的公路上以72km/h的速度匀速行驶,当发现前方有货车低速前进时,立刻刹车做匀减速运动,加速度大小为2.5m/s2.当速度减小到18km/h时,跟车匀速行驶,经过t=40s,货车转弯让道,救护车立刻以1.5m/s2的加速度匀加速恢复至原来速度.求:
(1)救护车从开始刹车到恢复至原来速度所经历的时间.
(2)与正常行驶相比,由于货车挡道,救护车多用了多少时间?
【答案】
分析:(1)救护车先匀减速直线运动,然后匀速直线运动,最后匀加速直线运动,根据速度时间关系公式求解出三段时间后求和即可;
(2)求解出三段位移后求和,假设正常行驶,求出时间,与实际时间相减得到多用的时间.
解答:解:(1)匀减速直线运动过程,根据速度时间关系公式,有:v
2=v
1+a
1t
1…①;
匀速直线运动过程时间为:t
=40s…②
匀加速直线运动过程,根据速度时间关系公式,有:v
1=v
2+a
2t
2…②
联立①②③解得:t
1=6s,t
2=10s;
故总时间为:t=t
1+t
+t
2=5+40+10=55s;
(2)匀减速直线运动过程,根据平均速度公式,其位移为:
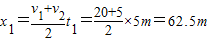
;
匀速直线运动过程,其位移为:x
=v
2t
=5×40=200m;
匀加速直线运动过程,根据平均速度公式,其位移为:
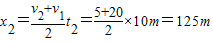
;
故总位移为:x=x
1+x
+x
2=62.5+200+125=387.5m;
若正常行驶,时间为:
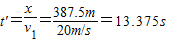
;
故多出的时间为:△t=t-t′=55s-19.375s=35.625s;
答:(1)救护车从开始刹车到恢复至原来速度所经历的时间为55s;
(2)与正常行驶相比,由于货车挡道,救护车多用了35.625s的时间.
点评:本题关键分析清楚小车的运动情况,然后分三个过程分别运用速度时间关系公式和位移时间关系公式列式后联立求解.

 ;
;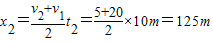 ;
;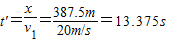 ;
;
