Question

（20分）一块平板玻璃放置在边长为2cm的玻璃立方体上，两者之间有一层平行的薄空气隙。波长在0.4μm到1.15μm之间的电磁波垂直入射到平板上，经空气隙的两边表面反射而发生干涉。在此波段中只有两种波长获得极大的增强，其一是₁＝0.4μm。求空气隙的厚度。

Answer 1

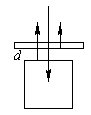
解析：光在厚度为d的空气隙中往返，经过的距离为2d。光被玻璃反射时，还经受180⁰的相位改变。于是对波长为₁的光，增强的条件为：

2d＝　（k₁＝0，1，2，3，……）

类似地，对其它波长的光，产生极大增强的条件是：

2d＝　（k₂＝0，1，2，3，……）

比较这两个条件，得到：

根据波长给定的范围，得到：

这个比值的最小可能值为1，最大可能值为2.875。因此我们得到关于k₁和k₂的下列条件：１＜＜2.875　　  （1）

对不同的k₁和k₂，我们算出上述分数值，得到下表：

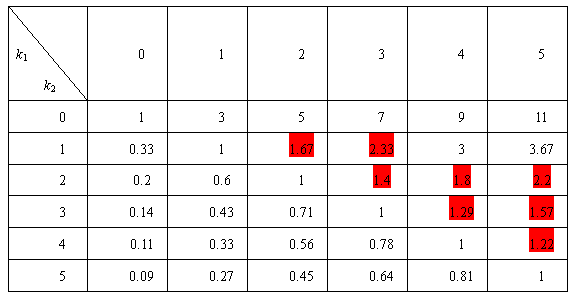
只有分数值满足条件（１）式的各个k₁和k₂对才是合格的，我们已在表格中算出。但其中只有一对是允许的。这就是说，我们应当找出这样的一列，其中只能有一对是允许的k₁和k₂。从表中看出，仅有的是k₁＝2，k₂＝1这一对，其分数值是1.67，这就是解答。

对于k₁＝0.4μm的光，根据2d＝2×0.4＋0.2＝1μm，得到空气隙的厚度为d＝0.5μm

由2×0.5＝

得到第二个波长为k₂＝0.667μm