
| H |
| sin37° |
| ||
| R |
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
| v | 2 C |
| ||
| r |
| H |
| sin37° |
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |


科目:高中物理 来源: 题型:
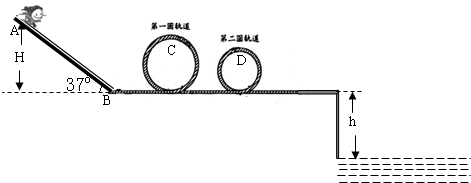
 如图所示,是某公园设计的一种游乐设施,所有轨道均光滑,AB面与水平面成一定夹角.一无动力小滑车质量为m=10kg,沿斜面轨道由静止滑下,然后滑入第一个圆形轨道内侧,其轨道半径R=2.5m,不计过B点的能量损失,根据设计要求,在圆轨道最低点与最高点各放一个压力传感器,测试小滑车对轨道的压力,并通过计算机显示出来.小滑车到达第一圆轨道最高点C处时刚好对轨道无压力,又经过水平轨道滑入第二个圆形轨道内侧,其轨道半径r=l.5m,然后从水平轨道上飞入水池内,水面离水平轨道的距离为h=5m.g取10m/s2,小滑车在运动全过程中可视为质点.求:
如图所示,是某公园设计的一种游乐设施,所有轨道均光滑,AB面与水平面成一定夹角.一无动力小滑车质量为m=10kg,沿斜面轨道由静止滑下,然后滑入第一个圆形轨道内侧,其轨道半径R=2.5m,不计过B点的能量损失,根据设计要求,在圆轨道最低点与最高点各放一个压力传感器,测试小滑车对轨道的压力,并通过计算机显示出来.小滑车到达第一圆轨道最高点C处时刚好对轨道无压力,又经过水平轨道滑入第二个圆形轨道内侧,其轨道半径r=l.5m,然后从水平轨道上飞入水池内,水面离水平轨道的距离为h=5m.g取10m/s2,小滑车在运动全过程中可视为质点.求:查看答案和解析>>
科目:高中物理 来源:2011-2012学年度浙江省杭州第十四中学高三物理上学期12月物理卷 题型:计算题
如图所示,是某公园设计的一种惊险刺激的娱乐设施,轨道CD部分粗糙,μ=0.1,其余均光滑。第一个圆管轨道的半径R=4m,第二个圆管轨道的半径r=3.6m。一挑战者质量m=60kg,沿斜面轨道滑下,滑入第一个圆管形轨道(假设转折处无能量损失),挑战者到达A、B两处最高点时刚好对管壁无压力,然后从平台上飞入水池内,水面离轨道的距离h=1m。g取10 m/s2,管的内径及人相对圆管轨道的半径可以忽略不计。则:
【小题1】挑战者若能完成上述过程,则他应从离水平轨道多高的地方开始下滑?
【小题2】CD部分的长度是多少?
【小题3】挑战者入水时的方向(用与水平方向夹角的正切值表示)?
查看答案和解析>>
科目:高中物理 来源:2013-2014学年浙江省高三上第一次阶段性测试物理试卷(解析版) 题型:计算题
(15分)如图所示,是某公园设计的一种惊险刺激的娱乐设施,轨道CD部分粗糙,μ=0.1,其余均光滑。第一个圆管轨道的半径R=4m,第二个圆管轨道的半径r=3.6m。一挑战者质量m=60kg,沿斜面轨道滑下,滑入第一个圆管形轨道(假设转折处无能量损失),挑战者到达A、B两处最高点时刚好对管壁无压力,然后从平台上飞入水池内,水面离轨道的距离h=1m。g取10 m/s2,管的内径忽略不计,人可视为质点。

求:(1)挑战者若能完成上述过程,则他应从离水平轨道多高的地方开始下滑?(2)CD部分的长度是多少?(3)挑战者入水时速度的大小和方向?
查看答案和解析>>
科目:高中物理 来源:2012届度浙江省高三物理上学期12月物理卷 题型:计算题
如图所示,是某公园设计的一种惊险刺激的娱乐设施,轨道CD部分粗糙,μ=0.1,其余均光滑。第一个圆管轨道的半径R=4m,第二个圆管轨道的半径r=3.6m。一挑战者质量m=60kg,沿斜面轨道滑下,滑入第一个圆管形轨道(假设转折处无能量损失),挑战者到达A、B两处最高点时刚好对管壁无压力,然后从平台上飞入水池内,水面离轨道的距离h=1m。g取10 m/s2,管的内径及人相对圆管轨道的半径可以忽略不计。则:

1.挑战者若能完成上述过程,则他应从离水平轨道多高的地方开始下滑?
2.CD部分的长度是多少?
3.挑战者入水时的方向(用与水平方向夹角的正切值表示)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com