
 如图所示,长L=6m的水平传输装置,在载物台左端物块以初速度v0=3m/s滑入传送带.物块与传送带之间的动摩擦因数μ=0.5,g=10m/s2,求:
如图所示,长L=6m的水平传输装置,在载物台左端物块以初速度v0=3m/s滑入传送带.物块与传送带之间的动摩擦因数μ=0.5,g=10m/s2,求: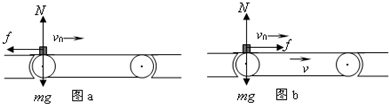
 =0.9m,
=0.9m,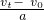 =
= s=0.6s
s=0.6s  =
= m=2.7m
m=2.7m =
= s=0.55s,
s=0.55s,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:
 如图所示,长L=6m的水平传输装置,在载物台左端物块以初速度v0=3m/s滑入传送带.物块与传送带之间的动摩擦因数μ=0.5,g=10m/s2,求:
如图所示,长L=6m的水平传输装置,在载物台左端物块以初速度v0=3m/s滑入传送带.物块与传送带之间的动摩擦因数μ=0.5,g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:2010-2011学年福建省漳州市高一(上)期末物理试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中物理 来源:2012年福建省泉州市南安三中高考物理一轮复习物理试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com