
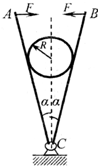
 一个重量为G的圆柱,半径为R,夹放在用铰链连接的两片夹板AC和BC之间,球心在C点正上方,如图所示.若圆柱和夹板之间的静摩擦因数为μ,水平力F的作用点A、B之间距离为l,角∠ACB=2α,若F太大或太小都会使圆柱体离开现在的位置,试求要使圆柱体在此位置平衡时力F的取值范围?
一个重量为G的圆柱,半径为R,夹放在用铰链连接的两片夹板AC和BC之间,球心在C点正上方,如图所示.若圆柱和夹板之间的静摩擦因数为μ,水平力F的作用点A、B之间距离为l,角∠ACB=2α,若F太大或太小都会使圆柱体离开现在的位置,试求要使圆柱体在此位置平衡时力F的取值范围?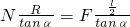
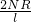 .
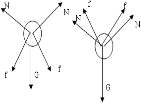
.
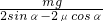 .
.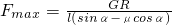 .
.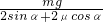
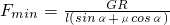 .
.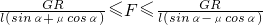 .
.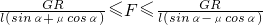 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com