
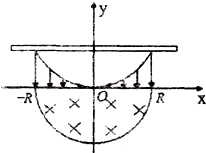
 如图所示,在一二象限-R≤x≤R范围内有竖直向下的匀强电场,场强大小为E,电场的上边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向里、边界方程为x2+y2=R2的匀强磁场.现在第二象限中电场的上边界分布有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.
如图所示,在一二象限-R≤x≤R范围内有竖直向下的匀强电场,场强大小为E,电场的上边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向里、边界方程为x2+y2=R2的匀强磁场.现在第二象限中电场的上边界分布有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.分析 (1)根据动能定理求出粒子经电场加速度后获得的速度,即进入磁场时速度.
(2)根据动能定理求出x=-$\frac{R}{3}$处的离子释放后获得的速度,然后运动学公式和牛顿第二定律求出从释放到经过点(R,0)所需时间t.
(3)所有离子都经过的点为持续发出荧光的点,由几何知识确定半径,由牛顿第二定律求磁感应强度.
解答 解:(1)当x=$-\frac{R}{2}$,y=$\frac{1}{2R}{x}^{2}$=$\frac{R}{8}$,
根据动能定理得,$qE\frac{R}{8}=\frac{1}{2}m{v}^{2}$,解得v=$\sqrt{\frac{qER}{4m}}$.
(2)当x=$-\frac{R}{3}$,y=$\frac{1}{2R}{x}^{2}=\frac{R}{18}$,
根据动能定理得,$qE\frac{R}{18}=\frac{1}{2}m{v}^{2}$,解得v=$\frac{1}{3}\sqrt{\frac{qER}{m}}$,
从释放到到达x轴时间为:t1=$\frac{v}{a}=\frac{\frac{1}{3}\sqrt{\frac{qER}{m}}}{\frac{qE}{m}}=\frac{1}{3}\sqrt{\frac{mR}{qE}}$.
a)第一种情况:离子直接从x=-$\frac{R}{3}$经磁场达x=R 处.
在磁场中经历半圆时间为:t2=$\frac{s}{v}$=$\frac{\frac{π}{2}(R+\frac{R}{3})}{v}$=$2π\sqrt{\frac{mR}{qE}}$,
总时间为:T1=t1+t2=(2π+$\frac{1}{3}$)$\sqrt{\frac{mR}{qE}}$,
b)第二种情况:离子直接从x=$-\frac{R}{3}$经磁场达x=$\frac{R}{3}$处进入电场返回磁场再到x=R处
易得在磁场中时间仍然为:t2=$2π\sqrt{\frac{mR}{qE}}$
在电场中时间为:3t1=$\sqrt{\frac{mR}{qE}}$,
总时间为:T2=3t1+t2=(2π+1)$\sqrt{\frac{mR}{qE}}$,
(3)在磁场B中有:qvB=$m\frac{{v}^{2}}{r}$,
所以运动半径为:r=$\frac{mv}{qB}$=$\frac{1}{B}\sqrt{\frac{mE}{qR}}|\begin{array}{l}{x}&{\;}\\{\;}&{\;}\end{array}|$,
可以看出,B一定时,必有r∝|x|,当|x|→0时,r→0 (离子经磁场偏转从逼近原点出磁场)因此,所有离子都从原点(0,0)点出磁场,击中荧光屏上(0,$\frac{1}{2}R$),
则有:2r=x
因为qvB1=m$\frac{{v}^{2}}{r}$
所以有:B1=$\frac{mv}{qr}$=$2\sqrt{\frac{mE}{qR}}$.
答:(1)横坐标为x=-$\frac{R}{2}$处的离子由静止释放后进入磁场时的速度大小为$\sqrt{\frac{qER}{4m}}$.
(2)从释放到经过点(R,0)所需时间为(2π+$\frac{1}{3}$)$\sqrt{\frac{mR}{qE}}$或(2π+1)$\sqrt{\frac{mR}{qE}}$.
(3)该点坐标和磁感应强度为$2\sqrt{\frac{mE}{qR}}$.
点评 本题中电场的区域边界是数学解析式的表达方式,设计新颖,学习中应该注意数学思想在物理中的应用.


科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 一半径为R的雨伞绕柄以角速度ω匀速旋转,如图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个半径为r的圆,则角速度的表达式为( )
一半径为R的雨伞绕柄以角速度ω匀速旋转,如图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个半径为r的圆,则角速度的表达式为( )| A. | $\frac{r-R}{R}$$\sqrt{\frac{g}{2h}}$ | B. | $\frac{1}{R}$$\sqrt{\frac{g({r}^{2}-{R}^{2})}{2h}}$ | C. | $\frac{r}{R}$$\sqrt{\frac{g}{2h}}$ | D. | $\frac{1}{R}$$\sqrt{\frac{g({r}^{2}+{R}^{2})}{2h}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
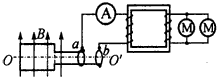 交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动.一小型发电机的线圈共220匝,线圈面积S=0.1m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$T.为用此发电机所发出交流电带动两个标有“220V 11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如图.求:
交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动.一小型发电机的线圈共220匝,线圈面积S=0.1m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$T.为用此发电机所发出交流电带动两个标有“220V 11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如图.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某游戏装置放在竖直平面内,如图所示,装置由粗糙抛物线形轨道AB和光滑的圆弧轨道BCD构成,控制弹射器可将穿在轨道上的小球以不同的水平初速度由A点射入,最后小球将由圆轨道的最高点D水平抛出,落入卡槽中得分,圆弧半径为R,O′为圆弧的圆心,C为圆弧轨道最低点,抛物线轨道上A点在坐标轴的原点O上,轨道与圆弧相切于B点,抛物线轨道方程为y=ax2(0<a<$\frac{1}{4R}$),∠BO′C=θ,x轴恰好将半径O′D分成相等的两半,交点为P,x轴与圆弧交于Q点,则:
某游戏装置放在竖直平面内,如图所示,装置由粗糙抛物线形轨道AB和光滑的圆弧轨道BCD构成,控制弹射器可将穿在轨道上的小球以不同的水平初速度由A点射入,最后小球将由圆轨道的最高点D水平抛出,落入卡槽中得分,圆弧半径为R,O′为圆弧的圆心,C为圆弧轨道最低点,抛物线轨道上A点在坐标轴的原点O上,轨道与圆弧相切于B点,抛物线轨道方程为y=ax2(0<a<$\frac{1}{4R}$),∠BO′C=θ,x轴恰好将半径O′D分成相等的两半,交点为P,x轴与圆弧交于Q点,则:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 只有受到一个方向不断改变的力,物体才可能做曲线运动 | |
| B. | 向心加速度是描述线速度大小变化快慢的物理量 | |
| C. | 物体做曲线运动时,其加速度一定改变 | |
| D. | 物体速度方向与所受合外力方向不在一条直线上,物体才可能做曲线运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com