
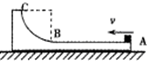
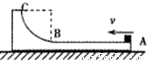
 如图,坚直平面内的轨道ABC由粗糙的水平滑道AB与光滑的四分之一圆弧滑道BC组成,AB恰与圆弧BC在B点相切,轨道放在光滑的水平面上,一个质量为1.0kg的小物块(可视为质点)从轨道的A端以8.0J的初动能水平冲上滑道AB,沿着轨道运动,由BC弧滑下后恰能停在水平滑道AB的中点,已知水平滑道AB长为2.0m,轨道ABC的质量为3.0kg,g=10m/s2.
如图,坚直平面内的轨道ABC由粗糙的水平滑道AB与光滑的四分之一圆弧滑道BC组成,AB恰与圆弧BC在B点相切,轨道放在光滑的水平面上,一个质量为1.0kg的小物块(可视为质点)从轨道的A端以8.0J的初动能水平冲上滑道AB,沿着轨道运动,由BC弧滑下后恰能停在水平滑道AB的中点,已知水平滑道AB长为2.0m,轨道ABC的质量为3.0kg,g=10m/s2.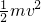 ,得
,得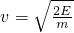 =4m/s
=4m/s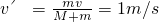



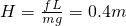


科目:高中物理 来源: 题型:
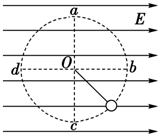 如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的质量为m的小球在竖直平面内做圆周运动(轨道半径为r),小球所受的电场力大小等于
如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的质量为m的小球在竖直平面内做圆周运动(轨道半径为r),小球所受的电场力大小等于| 3 |
查看答案和解析>>
科目:高中物理 来源:2012年安徽省蚌埠市高三第二次质检物理试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com