Question

（20分）火箭通过高速喷射燃气产生推力。设温度T₁、压强p₁的炽热高压气体在燃烧室内源源不断生成，并通过管道由狭窄的喷气口排入气压p₂的环境。假设燃气可视为理想气体，其摩尔质量为μ，每摩尔燃气的内能为u=c_VT（c_V是常量，T为燃气的绝对温度）。在快速流动过程中，对管道内任意处的两个非常靠近的横截面间的气体，可以认为它与周围没有热交换，但其内部则达到平衡状态，且有均匀的压强p、温度T和密度ρ，它们的数值随着流动而不断变化，并满足绝热方程（恒量），式中R为普适气体常量，求喷气口处气体的温度与相对火箭的喷射速率。

Answer 1

解析：

于火箭燃烧室出口处与喷气口各取截面与，它们的面积分别为和，由题意，，以其间管道内的气体为研究对象，如图所示．设经过很短时间，这部分气体流至截面与之间，间、间的微小体积分别为、，两处气体密度为、，流速为、．气流达到稳恒时，内部一切物理量分布只依赖于位置，与时间无关．由此可知，尽管间气体更换，但总的质量与能量不变。

   

先按绝热近似求喷气口的气体温度。质量守恒给出

，       (1)

即气体可视为由气体绝热移动所得．事实上，因气流稳恒，气体流出喷口时将再现气体状态．对质量的气体，利用理想气体的状态方程

                                              (2)

和绝热过程方程

，                       (3)

可得

．                                         (4)

再通过能量守恒求气体的喷射速率．由(1)式及，可得

，                                        (5)

再利用(1)、(3)式，知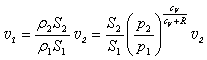，因， ，故

．                                                      (6)

整个体系经时间的总能量（包括宏观流动机械能与微观热运动内能）增量为部分与部分的能量差．由于重力势能变化可忽略，在理想气体近似下并考虑到(6)式，有

．                 (7)

体系移动过程中，外界做的总功为

．                                     (8)

根据能量守恒定律，绝热过程满足

，                                                      (9)

得

，           (10)

其中利用了(2)、(4)两式。

评分标准：本题20分。

（2)式1分，(3)式2分，(4)式3分，(6)式1分，(7)式6分，(8)式4分，(9)式1分，(10)式2分。