
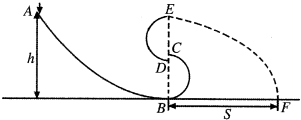
 如图所示,粗糙弧形轨道和两个光滑半圆形轨道组成翘S形尾巴的轨道.已知两个半圆轨道的半径均为R,端点B、C、D、E在同一竖直线上,连接处C、D间有较小空隙,刚好能够让小球通过,C、D间的距离可忽略.粗糙弧形轨道最高点A与圆形轨道最低点B的高度为h.从A点由静止释放一个可看做质点的小球,球过B点无能量损失,小球沿轨道运动后从E点水平飞出,落到水平地面上,落点F到B点的水平距离为s.已知小球的质量为m,不计空气阻力,求:
如图所示,粗糙弧形轨道和两个光滑半圆形轨道组成翘S形尾巴的轨道.已知两个半圆轨道的半径均为R,端点B、C、D、E在同一竖直线上,连接处C、D间有较小空隙,刚好能够让小球通过,C、D间的距离可忽略.粗糙弧形轨道最高点A与圆形轨道最低点B的高度为h.从A点由静止释放一个可看做质点的小球,球过B点无能量损失,小球沿轨道运动后从E点水平飞出,落到水平地面上,落点F到B点的水平距离为s.已知小球的质量为m,不计空气阻力,求:| 1 |
| 2 |
|
| v2 |
| R |
| s2 |
| 8R2 |
| s2 |
| 8R2 |
| 1 |
| 2 |
| mgs2 |
| 16R |
|
| s2 |
| 8R2 |
| mgs2 |
| 16R |


科目:高中物理 来源: 题型:
(15分) 如图所示是放置在竖直平面内游戏滑轨的装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为![]() 和
和![]()
![]() 的弧形轨道,倾斜直轨CD长为
的弧形轨道,倾斜直轨CD长为![]() 且表面粗糙,动摩擦因数为
且表面粗糙,动摩擦因数为![]() 其他三部分表面光滑,AB、CD与两圆形轨道相切.现有甲、乙两个质量为
其他三部分表面光滑,AB、CD与两圆形轨道相切.现有甲、乙两个质量为![]() 的小球穿在滑轨上,甲球静止在B点,乙球从AB的中点E处以
的小球穿在滑轨上,甲球静止在B点,乙球从AB的中点E处以![]() 的初速度水平向左运动,两球在整个过程中的碰撞均无能量损失.即甲乙两球每次发生碰撞后,甲、乙两球的速度都发生交换。已知
的初速度水平向左运动,两球在整个过程中的碰撞均无能量损失.即甲乙两球每次发生碰撞后,甲、乙两球的速度都发生交换。已知![]() (取
(取![]() 求:
求:
(1)甲球第一次通过⊙![]() 的最低点F处时对轨道的压力;
的最低点F处时对轨道的压力;
(2)小球每一次通过CD的过程中,克服摩擦力做的功;
(3) 在整个运动过程中,两球相撞次数;
(4) 两球分别通过CD段的总路程。
查看答案和解析>>
科目:高中物理 来源: 题型:
(08年西南师大附中月考)(16分)如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为R1 =1.0m和R2 = 3.0m的弧形轨道,倾斜直轨CD长为L = 6m且表面粗糙,动摩擦因数为μ =![]() ,其余部分表面光滑,AB、CD与两圆形轨道相切.现有甲、乙两个质量均为m = 2kg的小球穿在滑轨上,甲球静止在B点,乙球正以v0 = 10m/s的初速度水平向左运动如图所示.两球碰撞无能量损失。已知θ =37°,(取g=10m/s2,sin37°=0.6,cos37°= 0.8)求:
,其余部分表面光滑,AB、CD与两圆形轨道相切.现有甲、乙两个质量均为m = 2kg的小球穿在滑轨上,甲球静止在B点,乙球正以v0 = 10m/s的初速度水平向左运动如图所示.两球碰撞无能量损失。已知θ =37°,(取g=10m/s2,sin37°=0.6,cos37°= 0.8)求:
(1) 求乙球与甲球相碰后,甲球的速度;
(2) 甲球第一次通过圆O2的最低点F处时对轨道的压力大小;
(3) 判断甲球是否能再一次与乙球相撞,若能则求相撞前甲球的速度。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com