

���� 1��ʵ��ʱ������Ϊ����С�����������Ƶ���ɳ��ɳͰ������������ʵ�ʲ��ǣ�ʵ�ʵ�����Ϊ$\frac{mMg}{m+M}$��ֻ����M����m������½�����Ϊ��������mg��
2��B����ٶȿ���A��C���ƽ���ٶ���������ٶȿ����ȱ����˶��Ĺ��ɣ���x=at2��⣮
��� �⣺��1������С���ļ��ٶ�Ϊa������ΪF
��ɳͰ��ɳ��mg-F=ma����С����F=Ma��
�����ã�F=$\frac{mMg}{m+M}$=$\frac{mg}{1+\frac{m}{M}}$����ֻ����M����m������½�����Ϊ��������mg��
�����˵ķ�Ӧʱ����0.1s���ң���Ϊ��ߴ������Ч��ĸ�����Ӧ���Ƚ�ͨ��Դ��������ȶ����ٽ�ͨ��Դ��
��2��ֽ����ÿ��������������仹��4���㣬�������ڵļ�����֮���ʱ������T=0.1s��
�����������ٶȣ�
a=$\frac{15.06-6.75-6.75}{4��0.01}$=0.390m/s2��
�����ȱ���ֱ���˶����м�ʱ�̵�˲ʱ�ٶȵ��ڸù����е�ƽ���ٶȵã�
B����ٶ�Ϊ��vB=$\frac{10.71-3.18}{2��0.1}$=0.377m/s
�ʴ�Ϊ����1��M����m����2��0.390��0.377��
���� �ܹ�֪�����ڵļ�����֮���ʱ�����������ȱ���ֱ�ߵĹ����Լ����۽��ʵ���������������ƽʱ��ϰ��Ҫ��ǿ����֪ʶ��������Ӧ�ã���߽������������ֻҪ����������ʵ��ԭ������˳���������ʵ����Ŀ����ʵ�鲽�裬ʵ�����ݵĴ�������ʵ��ԭ���йأ���Ҫ��ǿ��ʵ��ԭ����ѧϰ�����գ�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������

| ��Ӧ�� | B | C | D | E | F |
| �ٶȣ�m/s�� | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���׳�����ع����У�����������������ƽ��������ͬ | |
| B�� | ���׳�����صĹ����У����������������Ĺ���ͬ | |
| C�� | ����С�����ǰ˲��Ķ�����ͬ | |
| D�� | ����С�����ǰ˲�䣬����������˲ʱ������ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
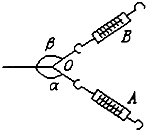 �ڡ�̽��������ķ�������ʵ���У�����ֻ���ɲ�����A��B��СԲ������ijһλ��O����ʱAO��BO��нǡ�AOB��90�㣬��ͼ��ʾ���ָı䵯�ɲ�����A����������ʹ���Ǽ�С�������ı������Ĵ�С����ôҪʹСԲ���Ա�����O�㣬��Ӧ���ڵ��ɲ�����B��������С���½ǣ������е��������У���Щ�ǿ��е� ��������
�ڡ�̽��������ķ�������ʵ���У�����ֻ���ɲ�����A��B��СԲ������ijһλ��O����ʱAO��BO��нǡ�AOB��90�㣬��ͼ��ʾ���ָı䵯�ɲ�����A����������ʹ���Ǽ�С�������ı������Ĵ�С����ôҪʹСԲ���Ա�����O�㣬��Ӧ���ڵ��ɲ�����B��������С���½ǣ������е��������У���Щ�ǿ��е� ��������| A�� | ����B��������ͬʱ����½� | B�� | ����B�����������֦½Dz��� | ||
| C�� | ����B��������С���䣬����½� | D�� | ����B��������ͬʱ��С�½� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
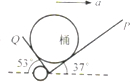 ��ˮԱ��˫��С������Ͱװˮ����5m/s2�ļ��ٶ�ˮƽ�����ȼ���ֱ���˶���С��������ˮƽ���37��ǣ���ͼ��ʾ����֪Ͱװˮ��������Ϊ20kg������Ͱ��С��֮���Ħ�����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8������˵����ȷ���ǣ�������
��ˮԱ��˫��С������Ͱװˮ����5m/s2�ļ��ٶ�ˮƽ�����ȼ���ֱ���˶���С��������ˮƽ���37��ǣ���ͼ��ʾ����֪Ͱװˮ��������Ϊ20kg������Ͱ��С��֮���Ħ�����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8������˵����ȷ���ǣ�������| A�� | С��P������Ͱ��֧������СΪ160N | |
| B�� | С��Q������Ͱ��֧������СΪ120N | |
| C�� | Ͱ��С����������ѹ����С֮��ΪFp��Fq=1��2 | |
| D�� | Ͱ��С����������ѹ����С֮��ΪFp��Fq=4��3 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | Ԫ��ɾ��ǵ��� | |
| B�� | Ԫ����DZ�ʾ��һ�������������������ֵ��ȵĵ���� | |
| C�� | Ԫ��ɾ������� | |
| D�� | ������������ֻ����Ԫ��ɵ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ͨ��ʵ�鷢���˵�Ÿ�Ӧ���� | |
| B�� | ��˹��ͨ��ʵ�鷢���˵�������ЧӦ | |
| C�� | ���ĵ���ͨ��Ť��ʵ�����˾��������� | |
| D�� | ��������������ˡ������ĸ���������Ե��á����ߡ�����������������������龰 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����v��2��$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$�� | B�� | 2$\frac{{{{����v��}^2}}}{{{x_2}-{x_1}}}$ | C�� | ����v��2��$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$�� | D�� | $\frac{{{{����v��}^2}}}{{{x_2}-{x_1}}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com