
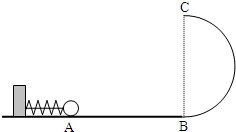
 (2009?烟台二模)如图所示,竖直放置的光滑半圆形轨道与光滑水平面AB相切于B点,半圆形轨道的最高点为C.轻弹簧一端固定在竖直挡板上,另一端有一质量为0.1kg的小球(小球与弹簧不相连).用力将小球向左推,小球将弹簧压缩一定量时用细绳固定住.此时弹簧的弹性势能为4.05J.烧断细绳,弹簧将小球弹出.取g=10m/s2,求
(2009?烟台二模)如图所示,竖直放置的光滑半圆形轨道与光滑水平面AB相切于B点,半圆形轨道的最高点为C.轻弹簧一端固定在竖直挡板上,另一端有一质量为0.1kg的小球(小球与弹簧不相连).用力将小球向左推,小球将弹簧压缩一定量时用细绳固定住.此时弹簧的弹性势能为4.05J.烧断细绳,弹簧将小球弹出.取g=10m/s2,求| 1 |
| 2 |
| v | 2 1 |
|
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| ||
| r |
| 81 |
| 50 |
| 81 |
| 50 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 3 |
| (8.1-4r)4r |
| 8.1 |
| 8 |


科目:高中物理 来源: 题型:
 (2009?烟台二模)一质量为m的滑块以初速度v0自固定在地面上的粗糙斜面的底端开始冲上斜面,到达某一高度后又自动返回至斜面底端,图中分别给出了在整个运动过程中滑块的速度v、加速度a、动能EK及重力势能EP随时间t的变化关系图线,则其中可能正确的是( )(规定斜面底端所在水平面为参考平面)
(2009?烟台二模)一质量为m的滑块以初速度v0自固定在地面上的粗糙斜面的底端开始冲上斜面,到达某一高度后又自动返回至斜面底端,图中分别给出了在整个运动过程中滑块的速度v、加速度a、动能EK及重力势能EP随时间t的变化关系图线,则其中可能正确的是( )(规定斜面底端所在水平面为参考平面)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com