C
分析:如果一个物体受到三个力的作用也能处于平衡状态,叫做三力平衡.是受力平衡中的一种.很显然这三个力的合力应该为零.而这三个力可能互成角度,也可能在一条直线上.
对于三力平衡,一般根据“任意两个力的合力与第三个力等大反向”的关系,借助三角函数、相似三角形等手段求解;或将某一个力分解到另外两个力的反方向上,得到的这两个分力势必与另外两个力等大、反向;对于多个力的平衡,利用先分解再合成的正交分解法.
本题对三物体受力分析,结合共点力平衡条件列式求解出F
1、F
2、F
3、F
4.
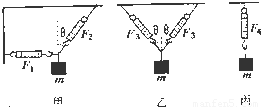
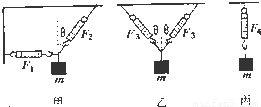
解答:对三物体分别受力分析,如图

根据三力平衡条件,三力中任意两个力的合力与第三个力等大反向,结合几何关系
F
1=mgtan30°=

mg
F
2=
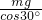
=

mg
F
3=

=

mg
F
4=mg
因而F
2最大;
故选C.
点评:物体在三个力的作用下处于平衡状态,要求我们分析三力之间的相互关系的问题叫三力平衡问题,这是物体受力平衡中最重要、最典型也最基础的平衡问题.这种类型的问题有以下几种常见题型:
①三个力中,有两个力互相垂直,第三个力角度(方向)已知.
②三个力互相不垂直,但夹角(方向)已知《考试说明》中规定力的合成与分解的计算只限于两力之间能构成直角的情形.三个力互相不垂直时,无论是用合成法还是分解法,三力组成的三角形都不是直角三角形,造成求解困难.因而这种类型问题的解题障碍就在于怎样确定研究方法上.解决的办法是采用正交分解法,将三个不同方向的力分解到两个互相垂直的方向上,再利用平衡条件求解.
③三个力互相不垂直,且夹角(方向)未知
三力方向未知时,无论是用合成法还是分解法,都找不到合力与分力之间的定量联系,因而单从受力分析图去求解这类问题是很难找到答案的.要求解这类问题,必须变换数学分析的角度,从我们熟悉的三角函数法变换到空间几何关系上去考虑,因而这种问题的障碍点是如何正确选取数学分析的方法.
解决这种类型的问题的对策是:首先利用合成法或分解法作出三力之间的平行四边形关系和三角形关系,再根据力的三角形寻找与之相似的空间三角形,利用三角形的相似比求解.
④三力的动态平衡问题 即三个力中,有一个力为恒力,另一个力方向不变,大小可变,第三个力大小方向均可变,分析第三个力的方向变化引起的物体受力的动态变化问题.

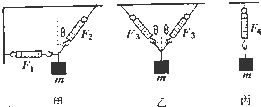 如图,用相同的弹簧秤将同一个重物m.分别按甲、乙、丙三种方式悬挂起来,读数分别是F1、F2、F3、F4,设θ=30°,则有
如图,用相同的弹簧秤将同一个重物m.分别按甲、乙、丙三种方式悬挂起来,读数分别是F1、F2、F3、F4,设θ=30°,则有
 mg
mg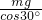 =
= mg
mg =
= mg
mg