
| A�� | ��Ϊv=$\sqrt{gR}$�����Ի����ٶ���R��������� | |
| B�� | ��Ϊv=$\sqrt{\frac{GM}{R}}$�����Ի����ٶ���R�������С | |
| C�� | ��ΪF=$\frac{GMm}{R2}$�����Ե�R����ԭ����2��ʱ�������������������Ϊԭ����$\frac{1}{4}$ | |
| D�� | ��ΪF=$\frac{m{v}^{2}}{R}$�����Ե�R����ԭ����2��ʱ�������������������Ϊԭ����$\frac{1}{2}$ |
���� ����������Բ���˶������������ṩ��������������뾶�仯ʱ�����������仯�����ǵ����ٶȡ����ٶȡ��������ű仯�����ԣ��������������ı���ʽ������һЩ�������ı仯��ע��������Ʊ�������
��� �⣺A��������뾶�仯ʱ����λ���������ٶ�Ҳ�ڱ仯�����Ը��ݹ�ʽv=$\sqrt{gR}$�������ٶ���R������������˵���Ǵ���ģ���A����
B�����ݹ�ʽv=$\sqrt{\frac{GM}{R}}$��֪��G��M���dz����������ٶ���R���������С����B��ȷ��
C�����ݹ�ʽF=$\frac{GMm}{{R}^{2}}$����R����ԭ����2��ʱ��M��m���䣬�������ǵ�������Ϊԭ����$\frac{1}{4}$����C��ȷ��
D�����ݹ�ʽv=$\sqrt{\frac{GM}{R}}$��֪����R����ԭ����2��ʱ��vΪԭ����$\frac{\sqrt{2}}{2}$����
���Ը��ݹ�ʽF=$\frac{m{v}^{2}}{R}$����R����ԭ����2��ʱ�����ǵ���������Ϊԭ����$\frac{1}{4}$����D����
��ѡ��BC
���� Բ���˶��Ĺ�ʽ�ı任����ʽ����ϸ��ͳһ��������һ����������������������������ⲻӦ������Ͳ²⣬��Ӧͨ��̤ʵ���Ƶ�������ȷ��ѡ���𰸣�


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ�������ƽ�еļ�����״��ȫ��ͬ������ƽ�н�����a��b��c��d���İ崹ֱ��ֽ����ã��İ峤��ΪL�����������ľ���ҲΪL�����Ȳ��ƣ�a��b����c��d������ͬ��С����ǿ�糡�����������糡�������Ҳ�����I���������II ���д�ֱ��ֽ�����ǿ�ų���ͼ��δ������������һ����Ϊm������Ϊq�������Ӵ�a��b �������е�O�ؼ����������Գ��ٶ�v����ƽ�н�����a��b��䣬ǡ�ô�a���Ҳ��Ե�����Ӵ����ɳ�����ų�����I�����ǡ�ܴ�d���Ҳ��Ե�����Ӵ�������c��d�䲢�� c��d������е�O���ؼ��������߽���ų������Ȼ��պûص�a��b�����O�����������˶���������������������
��ͼ��ʾ�������ƽ�еļ�����״��ȫ��ͬ������ƽ�н�����a��b��c��d���İ崹ֱ��ֽ����ã��İ峤��ΪL�����������ľ���ҲΪL�����Ȳ��ƣ�a��b����c��d������ͬ��С����ǿ�糡�����������糡�������Ҳ�����I���������II ���д�ֱ��ֽ�����ǿ�ų���ͼ��δ������������һ����Ϊm������Ϊq�������Ӵ�a��b �������е�O�ؼ����������Գ��ٶ�v����ƽ�н�����a��b��䣬ǡ�ô�a���Ҳ��Ե�����Ӵ����ɳ�����ų�����I�����ǡ�ܴ�d���Ҳ��Ե�����Ӵ�������c��d�䲢�� c��d������е�O���ؼ��������߽���ų������Ȼ��պûص�a��b�����O�����������˶����������������������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��ˮƽ�������ǿ�糡E=4V/m����ֱֽ���������ǿ�ų�B=2T������m=1g�Ĵ������С���A����M���ؾ�Ե�ֲڵ���ֱ�����ٻ��£�����0.8m��N��ʱ�뿪��ֱ���������˶�����P��ʱС���A˲ʱ����ƽ�⣬��ʱ�ٶ���ˮƽ�����45�㣮��P��N�ĸ߶Ȳ�Ϊ0.8m����
��ͼ��ʾ��ˮƽ�������ǿ�糡E=4V/m����ֱֽ���������ǿ�ų�B=2T������m=1g�Ĵ������С���A����M���ؾ�Ե�ֲڵ���ֱ�����ٻ��£�����0.8m��N��ʱ�뿪��ֱ���������˶�����P��ʱС���A˲ʱ����ƽ�⣬��ʱ�ٶ���ˮƽ�����45�㣮��P��N�ĸ߶Ȳ�Ϊ0.8m�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��1����ͼ����������ۻ����ߣ���ͼ��֪�������۵���t2���ۻ�ʱ��Ϊ��2����1��
��1����ͼ����������ۻ����ߣ���ͼ��֪�������۵���t2���ۻ�ʱ��Ϊ��2����1���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������ϸ����O�㴦��ᣬA��B���˹̶���ͬһˮƽ�������ΪL�������ϣ�ʹAOB��ֱ�������Σ���BAO=30�㣮��֪OC�߳���L���¶�C��ϵ��һ��С����С��뾶��������˵����ȷ���ǣ�������
��ͼ��ʾ������ϸ����O�㴦��ᣬA��B���˹̶���ͬһˮƽ�������ΪL�������ϣ�ʹAOB��ֱ�������Σ���BAO=30�㣮��֪OC�߳���L���¶�C��ϵ��һ��С����С��뾶��������˵����ȷ���ǣ�������| A�� | ��С����ֽ���ڰڶ�������T=2��$\sqrt{\frac{L}{g}}$ | |
| B�� | ��С���ڴ�ֱֽ�淽��ڶ�������T=2��$\sqrt{\frac{3L}{2g}}$ | |
| C�� | ��С����ֽ���ڰڶ�������T=2��$\sqrt{\frac{3L}{2g}}$ | |
| D�� | ��С���ڴ�ֱֽ���ڰڶ�������T=2��$\sqrt{\frac{L}{g}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��ʹ�ù��ܵ�ԭ��ͼ����Ƶ��Ϊv�Ŀɼ������䵽����K��ʱ�����������е���ͨ����
��ͼ��ʾ��ʹ�ù��ܵ�ԭ��ͼ����Ƶ��Ϊv�Ŀɼ������䵽����K��ʱ�����������е���ͨ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ���㹻�������Ϊ37��Ĺ̶�б�棬��A���Գ��ٶ�v0=2m/sˮƽ�׳�һ��С������B�㣬�������ٶ�Ϊg���������ڿ��з��е�ʱ��0.3s��AB���ˮƽ����Ϊ0.6m������֪��g=10m/s2��sin37��=0.6��cos37��=0.8��
��ͼ��ʾ��һ���㹻�������Ϊ37��Ĺ̶�б�棬��A���Գ��ٶ�v0=2m/sˮƽ�׳�һ��С������B�㣬�������ٶ�Ϊg���������ڿ��з��е�ʱ��0.3s��AB���ˮƽ����Ϊ0.6m������֪��g=10m/s2��sin37��=0.6��cos37��=0.8���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
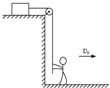 ��ͼ������Ϊm�����徲ֹ�ڹ⻬��ƽ̨�ϣ�ϵ�������ϵ����ӿ���⻬�Ķ����֣��ɵ����ϵ������������������ٶ�v0�߶�������������ֱ����н���0����45������У�������Ϊ��������
��ͼ������Ϊm�����徲ֹ�ڹ⻬��ƽ̨�ϣ�ϵ�������ϵ����ӿ���⻬�Ķ����֣��ɵ����ϵ������������������ٶ�v0�߶�������������ֱ����н���0����45������У�������Ϊ��������| A�� | $\frac{1}{2}$mv02 | B�� | $\frac{{\sqrt{2}}}{2}$mv02 | C�� | $\frac{1}{4}$mv02 | D�� | mv02 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com