
| A. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| B. | 在飞行试验器的工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器在工作轨道上的绕行速度为$\sqrt{g(R+h)}$ | |
| D. | 由题目条件可知月球的平均密度为$\frac{3g}{4πGR}$ |
分析 根据万有引力提供向心力,推导出线速度和角速度及周期的公式,得出选项.
解答 解:AC、根据万有引力提供向心力,即:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}}{{T}^{2}}r$,解得:$v=\sqrt{\frac{GM}{r}}$,$T=2π\sqrt{\frac{{r}^{3}}{GM}}$
飞行试验器的轨道半径为r=R+h,结合黄金代换公式:GM=gR2,代入线速度和周期公式得:$v=\sqrt{\frac{{R}^{2}g}{R+h}}$,$T=2π\sqrt{\frac{(R+h)^{3}}{g{R}^{2}}}$,故AC错误;
D、由黄金代换公式得中心天体的质量$M=\frac{g{R}^{2}}{G}$,月球的体积$V=\frac{4}{3}π{R}^{3}$,则月球的密度$ρ=\frac{3g}{4πGR}$,故D正确;
B、月球表面万有引力等于重力,则$G\frac{Mm}{(R+h)^{2}}=mg′$,得:$g′=(\frac{R}{R+h})^{2}g$,故B正确;
故选:BD
点评 本题关键根据卫星的万有引力等于向心力,以及星球表面重力等于万有引力列两个方程求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:解答题
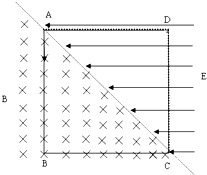 如图所示,在边长为a的正方形ABCD的对角线AC左右两侧,分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场,AD、CD是两块固定荧光屏(能吸收打到屏上的粒子).现有一群质量为m、电量为q的带正电粒子,从A点沿AB方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为$\frac{aqB}{12cm}$≤v≤$\frac{aq{B}^{2}}{m}$.已知E=$\frac{aq{B}^{2}}{12m}$,不计带电粒子的重力和粒子之间的相互作用.求:
如图所示,在边长为a的正方形ABCD的对角线AC左右两侧,分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场,AD、CD是两块固定荧光屏(能吸收打到屏上的粒子).现有一群质量为m、电量为q的带正电粒子,从A点沿AB方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为$\frac{aqB}{12cm}$≤v≤$\frac{aq{B}^{2}}{m}$.已知E=$\frac{aq{B}^{2}}{12m}$,不计带电粒子的重力和粒子之间的相互作用.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{a}_{1}+{a}_{2}}{2}$ | B. | $\frac{{m}_{1}{a}_{1}}{{m}_{1}+{m}_{2}}$ | C. | $\frac{{m}_{2}{a}_{2}}{{m}_{1}+{m}_{2}}$ | D. | $\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
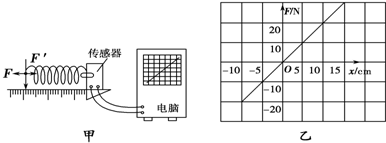
| A. | 弹簧产生的弹力和弹簧的长度成正比 | |
| B. | 弹簧长度的增加量与对应的弹力增加量成正比 | |
| C. | 该弹簧的劲度系数是200 N/m | |
| D. | 该弹簧受到反向压力时,劲度系数不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
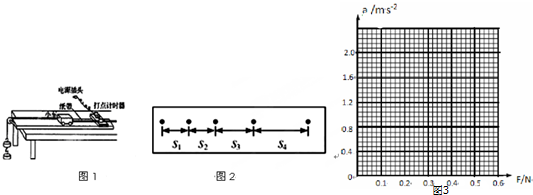
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/m•s-2 | 0.25 | 0.57 | 0.89 | 1.20 | 1.52 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
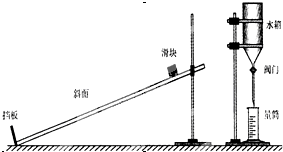 伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.某校物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.
伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.某校物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| S(m) | 4.5 | 3.9 | 3.0 | 2.1 | 1.5 | 0.9 | 0.3 |
| V(mL) | 90 | 84 | 72 | 62 | 52 | 40 | 23.5 |
| $\frac{S}{{V}^{2}}$×10-4 | 5.6 | 5.5 | 5.8 | 5.5 | 5.6 | 5.6 | 5.4 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
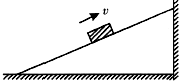 如图所示,质量为M的斜劈靠墙放置,质量为m的滑块以一定的初速度滑上斜劈,只考虑滑块与斜面间的摩擦,不计其它接触面之间的摩擦,则在滑块上滑的过程中( )
如图所示,质量为M的斜劈靠墙放置,质量为m的滑块以一定的初速度滑上斜劈,只考虑滑块与斜面间的摩擦,不计其它接触面之间的摩擦,则在滑块上滑的过程中( )| A. | 地面对斜劈的支持力大于(M+m)g | B. | 地面对斜劈的支持力小于(M+m)g | ||
| C. | 墙壁对斜劈的弹力大小在逐渐减小 | D. | 墙壁对斜劈的弹力大小始终不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
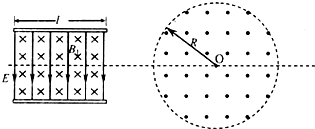
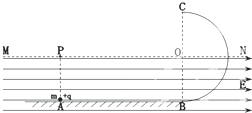 如图所示,光滑绝缘水平轨道与半径为R的光滑绝缘竖直半圆轨道在B点平滑连接.在过圆心O的水平界面的下方分布有水平向右的匀强电场.现有一个质量为m、电量为+q的小球从水平轨道上的A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,小球可视为质点,小球运动过程中电量保持不变).已知A、B间的距离为2R,重力加速度为g,在上述运动过程中,求:
如图所示,光滑绝缘水平轨道与半径为R的光滑绝缘竖直半圆轨道在B点平滑连接.在过圆心O的水平界面的下方分布有水平向右的匀强电场.现有一个质量为m、电量为+q的小球从水平轨道上的A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,小球可视为质点,小球运动过程中电量保持不变).已知A、B间的距离为2R,重力加速度为g,在上述运动过程中,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com