Question

14．如图甲所示的平面直角坐标系xoy中，整个区域内存在匀强磁场，磁感应强度B随时间t的变化关系如图乙所示，（垂直纸面向里为正），t=0时刻，有一个带正电的粒子（不计重力）从坐标原点0沿x轴正方向进入磁场，初速度为v₀=2.0×10³m/s，已知带电粒子的比荷为1.0×10⁴C/kg，试求：
（1）t=$\frac{4π}{3}$×10^-4s时刻，粒子的位置坐标；
（2）粒子从开始时刻起经过多长时间到达y轴；
（3）粒子返回原点所经历的时间．

Answer 1

分析 （1）画出运动轨迹，由洛伦兹力提供向心力得半径和周期，根据时间知转过的角度，根据几何知识求解位置坐标；
（2）根据周期和角度分别求出各段时间从而求总时间；
（3）粒子在磁场中作周期性运动，根据对称性和周期性，画出粒子运动的轨迹，根据周期和角度分别求出各段时间从而求总时间．

解答 解：（1）粒子进入磁场后在磁场中作匀速圆周运动，设半径为R，周期为T，
由洛伦兹力提供向心力得：$Bqv=m\frac{v^2}{R}$…①
$R=\frac{mv}{Bq}=0.4m$…②
$T=\frac{2πm}{Bq}=4π×{10^{-4}}s$…③
${t_1}=\frac{1}{3}T$
得θ₁=120°
转到A点，如图甲所示，则A点的坐标为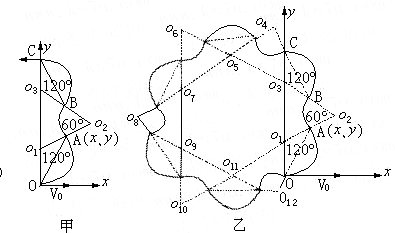
$x=Rcos30°=0.2\sqrt{3}m$…④
$y=R+\overline{{O_1}A}sin30°=0.6m$…⑤
（2）由图甲知
${t_1}=\frac{1}{3}T$…⑥
${t_2}=\frac{1}{6}T$…⑦
${t_3}=\frac{1}{3}T$…⑧
由③⑥⑦⑧得$t={t_1}+{t_2}+{t_3}=\frac{10π}{3}×{10^{-4}}s$…⑨
（3）粒子在磁场中作周期性运动，根据对称性和周期性，画出粒子运动的轨迹如图乙所示，
其中O₂、O₆、O₁₀构成一个正三角形，故粒子从开始到返回坐标原点的总时间为：$T=6×\frac{4π}{3}×{10^{-4}}s+6×\frac{2π}{3}×{10^{-4}}s=12π×{10^{-4}}$s   …⑩
答：（1）t=$\frac{4π}{3}$×10^-4s时刻，粒子的位置坐标（0.2$\sqrt{3}$m，0.6m）；
（2）粒子从开始时刻起经过$\frac{10π}{3}×1{0}^{-4}$s到达y轴；
（3）粒子返回原点所经历的时间为12π×10^-4s．

点评 本题主要考查了带电粒子在混合场中运动的问题，要求同学们能正确分析粒子的受力情况，再通过受力情况分析粒子的运动情况，画出运动过程图，熟练掌握圆周运动的基本公式，难度适中．