
 »γΆΦΘ®aΘ©Υυ ΨΘ§AΓΔBΈΣΕΛ‘ΎΙβΜ§Υ°ΤΫΟφ…œΒΡΝΫΗυΧζΕΛΘ§–Γ«ρC”Ο≥ΛΈΣlΒΡœΗ…ΰΥ©‘ΎΧζΕΛB…œΘ®œΗ…ΰΡή≥– ήΉψΙΜ¥σΒΡά≠ΝΠΘ©Θ§AΓΔBΓΔC‘ΎΆ§“Μ÷±œΏ…œΘ§t=0 ±Θ§Ηχ–Γ«ρ“ΜΗω¥Ι÷±”Ύ…ΰΒΡΥΌΕ»Θ§ Ι–Γ«ρ»ΤΉ≈ΝΫΗυΧζΕΛ‘ΎΥ°ΤΫΟφ…œΉω‘≤÷ή‘ΥΕ·Θ§‘Ύ0ΓήtΓή10s ±ΦδΡΎΘ§œΗ…ΰΒΡά≠ΝΠΥφ ±Φδ±δΜ·ΒΡΙφ¬…»γΆΦΘ®bΘ©Υυ ΨΘ§ ‘«σΘΚ
»γΆΦΘ®aΘ©Υυ ΨΘ§AΓΔBΈΣΕΛ‘ΎΙβΜ§Υ°ΤΫΟφ…œΒΡΝΫΗυΧζΕΛΘ§–Γ«ρC”Ο≥ΛΈΣlΒΡœΗ…ΰΥ©‘ΎΧζΕΛB…œΘ®œΗ…ΰΡή≥– ήΉψΙΜ¥σΒΡά≠ΝΠΘ©Θ§AΓΔBΓΔC‘ΎΆ§“Μ÷±œΏ…œΘ§t=0 ±Θ§Ηχ–Γ«ρ“ΜΗω¥Ι÷±”Ύ…ΰΒΡΥΌΕ»Θ§ Ι–Γ«ρ»ΤΉ≈ΝΫΗυΧζΕΛ‘ΎΥ°ΤΫΟφ…œΉω‘≤÷ή‘ΥΕ·Θ§‘Ύ0ΓήtΓή10s ±ΦδΡΎΘ§œΗ…ΰΒΡά≠ΝΠΥφ ±Φδ±δΜ·ΒΡΙφ¬…»γΆΦΘ®bΘ©Υυ ΨΘ§ ‘«σΘΚΖ÷Έω Θ®1Θ©ΗυΨίά≠ΝΠΧαΙ©œρ–ΡΝΠΘ§ΫαΚœΆΦœΏΘ§Ά®Ιΐά≠ΝΠΒΡ±δΜ·ΒΟ≥ωΉΣΕ·ΑκΨΕΒΡ±δΜ·Θ§¥”ΕχΒΟ≥ωΝΫΕΛΉ”ΦδΒΡΨύάκdΘ°
Θ®2Θ©ΉΞΉΓΉΣΕ·ΒΡœΏΥΌΕ»≤Μ±δΘ§ΫαΚœΑκΨΕΒΡ±δΜ·ΒΟ≥ωΟΩ“ΜΗωΑκ»ΠΒΡ ±ΦδΘ§¥”Εχ»ΖΕ®≥ωt=14s ±ΉΣΕ·ΒΡΑκΨΕΘ§ΫαΚœά≠ΝΠΧαΙ©œρ–ΡΝΠΘ§Ά®Ιΐ±»ΫœΒΟ≥ωά≠ΝΠΒΡ¥σ–ΓΘ°
Θ®3Θ©ΉΞΉΓΟΩΉΣΕ·Ακ»ΠΘ§…ΰ≥Λ…Ό$\frac{1}{6}l$Θ§‘ρ ±Φδ…Ό$\frac{1}{6}t$Θ§»ΖΕ®≥ωœΗ…ΰΒΎ»ΐ¥Έ≈ωΕΛΉ”ΒΫΒΎΥΡ¥Έ≈ωΕΛΉ”ΒΡ ±ΦδΦδΗτΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©0-6sΡΎΘ§…ΰΉ”ΒΡά≠ΝΠ≤Μ±δΘ§${F}_{1}=m\frac{{v}^{2}}{l}$Θ§
6-10sΡΎά≠ΝΠ¥σ–Γ≤Μ±δΘ§${F}_{2}=m\frac{{v}^{2}}{{l}_{1}}$Θ§
“ρΈΣ${F}_{2}=\frac{6}{5}{F}_{1}$Θ§‘ρ${l}_{1}=\frac{5}{6}l$Θ§
Ω…÷ΣΝΫΕΛΉ”ΦδΒΡΨύάκd=$l-{l}_{1}=\frac{1}{6}l$Θ°
Θ®2Θ©ΒΎ“ΜΗωΑκ»ΠΨ≠άζΒΡ ±ΦδΈΣ6sΘ§‘ρ${t}_{1}=\frac{Π–l}{v}=6s$
‘ρΒΎΕΰΗωΑκ»ΠΒΡ ±Φδ${t}_{2}=\frac{Π–lΓδ}{v}=\frac{5}{6}{t}_{1}=5s$Θ§
–Γ«ρΉΣΒΎ»ΐΗωΑκ»ΠΒΡ ±Φδ${t}_{3}=\frac{Π–{l}_{2}}{v}$=$\frac{2}{3}{t}_{1}=4s$Θ§
‘ρt=14s ±Θ§–Γ«ρΉΣΕ·ΒΡΑκΨΕr=$\frac{2}{3}l$Θ§
œΗ…ΰΒΡά≠ΝΠ${F}_{3}=m\frac{{v}^{2}}{r}=\frac{3}{2}ΓΝ\frac{m{v}^{2}}{l}=\frac{3}{2}ΓΝ5N=7.5N$Θ°
Θ®3Θ©”…Χβ“β÷ΣΘ§œΗ…ΰΟΩΗζΕΛΉ”≈ωΉ≤“Μ¥ΈΘ§ΉΣΕ·Ακ»ΠΒΡ ±Φδ…Ό$\frac{1}{6}t=1s$Θ§
‘ρœΗ…ΰΒΎ»ΐ¥Έ≈ωΕΛΉ”ΒΫΒΎΥΡ¥Έ≈ωΕΛΉ”ΒΡ ±ΦδΦδΗτΓςt®T6-3ΓΝ1=3sΘ°
¥πΘΚΘ®1Θ©ΝΫΕΛΉ”ΦδΒΡΨύάκdΈΣ$\frac{1}{6}l$ΘΜ
Θ®2Θ©t=14s ±œΗ…ΰά≠ΝΠΒΡ¥σ–ΓΈΣ7.5NΘΜ
Θ®3Θ©œΗ…ΰΒΎ»ΐ¥Έ≈ωΕΛΉ”ΒΫΒΎΥΡ¥Έ≈ωΕΛΉ”ΒΡ ±ΦδΦδΗτΈΣ3sΘ°
ΒψΤά ΫβΨω±ΨΧβΒΡΙΊΦϋ÷ΣΒά…ΰΉ”ΒΡά≠ΝΠΧαΙ©‘≤÷ή‘ΥΕ·ΒΡœρ–ΡΝΠΘ§‘ΎΗζΕΛΉ”≈ωΉ≤ΒΡΙΐ≥Χ÷–Θ§–Γ«ρΒΡœΏΥΌΕ»¥σ–Γ≤Μ±δΘ§ΉΣΕ·ΒΡΑκΨΕΟΩΉΣΕ·Ακ»Π±δΜ·“Μ¥ΈΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
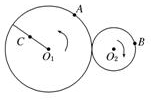 »γΆΦΥυ ΨΘ§ΩΩΡΠ≤Ν¥ΪΕ·Ήω‘»ΥΌΉΣΕ·ΒΡ¥σΓΔ–ΓΝΫ¬÷Ϋ”¥ΞΟφΜΞ≤Μ¥ρΜ§Θ§¥σ¬÷ΑκΨΕ «–Γ¬÷ΑκΨΕΒΡ2±ΕΘ§AΓΔBΖ÷±πΈΣ¥σΓΔ–Γ¬÷±Ώ‘Β…œΒΡΒψΘ§CΈΣ¥σ¬÷…œ“ΜΧθΑκΨΕΒΡ÷–ΒψΘ§‘ρΘ®ΓΓΓΓΘ©
»γΆΦΥυ ΨΘ§ΩΩΡΠ≤Ν¥ΪΕ·Ήω‘»ΥΌΉΣΕ·ΒΡ¥σΓΔ–ΓΝΫ¬÷Ϋ”¥ΞΟφΜΞ≤Μ¥ρΜ§Θ§¥σ¬÷ΑκΨΕ «–Γ¬÷ΑκΨΕΒΡ2±ΕΘ§AΓΔBΖ÷±πΈΣ¥σΓΔ–Γ¬÷±Ώ‘Β…œΒΡΒψΘ§CΈΣ¥σ¬÷…œ“ΜΧθΑκΨΕΒΡ÷–ΒψΘ§‘ρΘ®ΓΓΓΓΘ©| AΘ° | ΝΫ÷ ΒψΒΡœΏΥΌΕ»vA=2vB | BΘ° | ΝΫ¬÷ΉΣΕ·ΒΡΫ«ΥΌΕ»œύΒ» | ||
| CΘ° | –Γ¬÷ΉΣΕ·ΒΡΫ«ΥΌΕ» «¥σ¬÷ΒΡ2±Ε | DΘ° | ÷ ΒψΦ”ΥΌΕ»aB=aC |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚΕύ―ΓΧβ
| AΘ° | ‘Ύt=2s ±ΒΡΥΌΕ»ΈΣ6m/s | |
| BΘ° | ‘Ύt=4s ±ΒΡΥΌΕ»ΈΣ11m/s | |
| CΘ° | ’βΗωΈοΧε‘ΥΕ·ΒΡΦ”ΥΌΕ»ΈΣa=2.25m/s2 | |
| DΘ° | ’βΗωΈοΧε‘ΥΕ·ΒΡ≥θΥΌΕ»ΈΣv0=1.5m/s |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚΦΤΥψΧβ
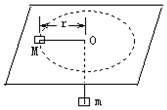 »γΆΦΥυ ΨΘ§œΗ…ΰ“ΜΕΥœΒΉ≈÷ ΝΩM=2kgΒΡΈοΧεΘ§Ψ≤÷Ι‘ΎΥ°ΤΫΟφΘ§Νμ“ΜΕΥΆ®ΙΐΙβΜ§–ΓΩΉΒθΉ≈÷ ΝΩm=0.3kgΒΡΈοΧεΘ§MΒΡ÷–Βψ”κ‘≤ΩΉΨύάκΈΣ0.2mΘ§≤Δ÷ΣMΚΆΥ°ΤΫΟφΒΡΉν¥σΨ≤ΡΠ≤ΝΝΠΈΣ7NΘ§œ÷ Ι¥ΥΤΫΟφ»Τ÷––Ρ÷αΉΣΕ·Θ§Έ Ϋ«ΥΌΕ»ΠΊ‘Ύ ≤Ο¥ΖΕΈßΡΎmΜα¥Π”ΎΨ≤÷ΙΉ¥Χ§ΘΩg»Γ10m/s2Θ°
»γΆΦΥυ ΨΘ§œΗ…ΰ“ΜΕΥœΒΉ≈÷ ΝΩM=2kgΒΡΈοΧεΘ§Ψ≤÷Ι‘ΎΥ°ΤΫΟφΘ§Νμ“ΜΕΥΆ®ΙΐΙβΜ§–ΓΩΉΒθΉ≈÷ ΝΩm=0.3kgΒΡΈοΧεΘ§MΒΡ÷–Βψ”κ‘≤ΩΉΨύάκΈΣ0.2mΘ§≤Δ÷ΣMΚΆΥ°ΤΫΟφΒΡΉν¥σΨ≤ΡΠ≤ΝΝΠΈΣ7NΘ§œ÷ Ι¥ΥΤΫΟφ»Τ÷––Ρ÷αΉΣΕ·Θ§Έ Ϋ«ΥΌΕ»ΠΊ‘Ύ ≤Ο¥ΖΕΈßΡΎmΜα¥Π”ΎΨ≤÷ΙΉ¥Χ§ΘΩg»Γ10m/s2Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚΕύ―ΓΧβ
 »γΆΦΥυ ΨΘ§≥ΛΈΣ l ΒΡ«αΗΥΘ§“ΜΕΥΙΧΕ®“ΜΗω–Γ«ρΘ§Νμ“ΜΕΥΙΧΕ®‘ΎΙβΜ§ΒΡΥ°ΤΫ÷α…œΘ§ Ι–Γ«ρ ‘Ύ ζ÷±ΤΫΟφΡΎΉω‘≤÷ή‘ΥΕ·Θ§ΙΊ”Ύ–Γ«ρ‘ΎΉνΗΏΒψΒΡΥΌΕ» vΘ§œ¬Ν––π ω’ΐ»ΖΒΡ «Θ®÷ΊΝΠΦ”ΥΌΕ» ΈΣ gΘ©Θ®ΓΓΓΓΘ©
»γΆΦΥυ ΨΘ§≥ΛΈΣ l ΒΡ«αΗΥΘ§“ΜΕΥΙΧΕ®“ΜΗω–Γ«ρΘ§Νμ“ΜΕΥΙΧΕ®‘ΎΙβΜ§ΒΡΥ°ΤΫ÷α…œΘ§ Ι–Γ«ρ ‘Ύ ζ÷±ΤΫΟφΡΎΉω‘≤÷ή‘ΥΕ·Θ§ΙΊ”Ύ–Γ«ρ‘ΎΉνΗΏΒψΒΡΥΌΕ» vΘ§œ¬Ν––π ω’ΐ»ΖΒΡ «Θ®÷ΊΝΠΦ”ΥΌΕ» ΈΣ gΘ©Θ®ΓΓΓΓΘ©| AΘ° | vΒΡΦΪ–Γ÷ΒΈΣgl | |
| BΘ° | v”…Νψ÷πΫΞ‘ω¥σ ±Θ§œρ–ΡΝΠ“≤÷πΫΞ‘ω¥σ | |
| CΘ° | Β±v”…$\sqrt{gl}$÷πΫΞ‘ω¥σ ±Θ§ΗΥΕ‘–Γ«ρΒΡΒ·ΝΠ“≤÷πΫΞ‘ω¥σ | |
| DΘ° | Β±v”…$\sqrt{gl}$÷πΫΞΦθ–Γ ±Θ§ΗΥΕ‘–Γ«ρΒΡΒ·ΝΠ“≤÷πΫΞΦθ–Γ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
 »γΆΦΥυ ΨΘ§‘ΎΟΉ≥ΏΒΡ“ΜΕΥΉξ“ΜΗω–ΓΩΉΘ§ Ι–ΓΩΉ«ΓΡή¥©Ιΐ“ΜΗυœΗœΏΘ§œΏœ¬ΕΥΙ““Μ÷ ΝΩΈΣmΒΡ–ΓΗ÷«ρΘ® ”ΈΣ÷ ΒψΘ©Θ°ΫΪΟΉ≥ΏΙΧΕ®‘ΎΥ°ΤΫΉάΟφ…œΘ§ ΙΗ÷«ρ‘ΎΥ°ΤΫΟφΡΎΉω‘»ΥΌ‘≤÷ή‘ΥΕ·Θ§‘≤–ΡΈΣOΘ§¥ΐΗ÷«ρΒΡ‘ΥΕ·Έ»Ε®ΚσΘ§ΕΝ≥ωΗ÷«ρΒΫOΒψΒΡΨύάκrΘ§≤Δ”ΟΟκ±μ≤βΝΩ≥ωΗ÷«ρΉΣΕ·n»Π”ΟΒΡ ±ΦδtΘ°‘ρΘΚ
»γΆΦΥυ ΨΘ§‘ΎΟΉ≥ΏΒΡ“ΜΕΥΉξ“ΜΗω–ΓΩΉΘ§ Ι–ΓΩΉ«ΓΡή¥©Ιΐ“ΜΗυœΗœΏΘ§œΏœ¬ΕΥΙ““Μ÷ ΝΩΈΣmΒΡ–ΓΗ÷«ρΘ® ”ΈΣ÷ ΒψΘ©Θ°ΫΪΟΉ≥ΏΙΧΕ®‘ΎΥ°ΤΫΉάΟφ…œΘ§ ΙΗ÷«ρ‘ΎΥ°ΤΫΟφΡΎΉω‘»ΥΌ‘≤÷ή‘ΥΕ·Θ§‘≤–ΡΈΣOΘ§¥ΐΗ÷«ρΒΡ‘ΥΕ·Έ»Ε®ΚσΘ§ΕΝ≥ωΗ÷«ρΒΫOΒψΒΡΨύάκrΘ§≤Δ”ΟΟκ±μ≤βΝΩ≥ωΗ÷«ρΉΣΕ·n»Π”ΟΒΡ ±ΦδtΘ°‘ρΘΚ≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚΦΤΥψΧβ
 »γΆΦΥυ ΨΘ§ΉΑ÷ΟBOΓδOΩ…»Τ ζ÷±÷αOΓδOΉΣΕ·Θ§Ω… ”ΈΣ÷ ΒψΒΡ–Γ«ρA”κΝΫœΗœΏΝ§Ϋ”ΚσΖ÷±πœΒ”ΎBΓΔCΝΫΒψΘ§ΉΑ÷ΟΨ≤÷ΙABΥ°ΤΫΘ§œΗœΏAC”κ ζ÷±ΖΫœρΒΡΦ–Ϋ«Π»=37ΓψΘ°“―÷Σ–Γ«ρΒΡ÷ ΝΩm=1kgΘ§œΗœΏAC≥Λl=0.5mΘ§BΒψΨύCΒψΒΡΥ°ΤΫΨύάκΚΆ ζ÷±ΨύάκœύΒ»Θ§Θ®÷ΊΝΠΦ”ΥΌΕ»g»Γ10m/s2Θ§sin37Γψ=$\frac{3}{5}$Θ§cos37Γψ=$\frac{4}{5}$Θ©Θ°
»γΆΦΥυ ΨΘ§ΉΑ÷ΟBOΓδOΩ…»Τ ζ÷±÷αOΓδOΉΣΕ·Θ§Ω… ”ΈΣ÷ ΒψΒΡ–Γ«ρA”κΝΫœΗœΏΝ§Ϋ”ΚσΖ÷±πœΒ”ΎBΓΔCΝΫΒψΘ§ΉΑ÷ΟΨ≤÷ΙABΥ°ΤΫΘ§œΗœΏAC”κ ζ÷±ΖΫœρΒΡΦ–Ϋ«Π»=37ΓψΘ°“―÷Σ–Γ«ρΒΡ÷ ΝΩm=1kgΘ§œΗœΏAC≥Λl=0.5mΘ§BΒψΨύCΒψΒΡΥ°ΤΫΨύάκΚΆ ζ÷±ΨύάκœύΒ»Θ§Θ®÷ΊΝΠΦ”ΥΌΕ»g»Γ10m/s2Θ§sin37Γψ=$\frac{3}{5}$Θ§cos37Γψ=$\frac{4}{5}$Θ©Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
 »γΆΦΥυ ΨΘ§»Υ”Ο…ΰΉ”Ά®ΙΐΕ·Μ§¬÷ά≠AΘ§A¥©‘ΎΙβΜ§ΒΡ ζ÷±ΗΥ…œΘ§»τ»Υ‘»ΥΌœρœ¬ά≠…ΰ ΙΈοΧεA―ΊΗΥœρ…œ‘ΥΕ·Θ§‘ρΈοΧεAΉςΚΈ‘ΥΕ·Θ®ΓΓΓΓΘ©
»γΆΦΥυ ΨΘ§»Υ”Ο…ΰΉ”Ά®ΙΐΕ·Μ§¬÷ά≠AΘ§A¥©‘ΎΙβΜ§ΒΡ ζ÷±ΗΥ…œΘ§»τ»Υ‘»ΥΌœρœ¬ά≠…ΰ ΙΈοΧεA―ΊΗΥœρ…œ‘ΥΕ·Θ§‘ρΈοΧεAΉςΚΈ‘ΥΕ·Θ®ΓΓΓΓΘ©| AΘ° | ‘»ΥΌ | BΘ° | Φ”ΥΌ | CΘ° | ΦθΥΌ | DΘ° | ΈόΖ®»ΖΕ® |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷–Έοάμ ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ΙΠ¬ «Οη ωΝΠΕ‘ΈοΧεΉωΙΠΕύ…ΌΒΡΈοάμΝΩ | |
| BΘ° | ΝΠΉωΙΠ ±Φδ‘Ϋ≥ΛΘ§ΝΠΒΡΙΠ¬ ‘Ϋ–Γ | |
| CΘ° | ”…P=$\frac{W}{t}$÷ΣΘ§ΙΠ¬ Β»”ΎΒΞΈΜ ±ΦδΡΎΝΠΉωΒΡΙΠ | |
| DΘ° | ”…P=Fv÷ΣΘ§ΝΠ‘Ϋ¥σΘ§ΉωΙΠ‘ΫΩλ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com