一质量为4kg的物体静止在粗糙的地面上,物体与地面的动摩擦因数为0.2,用一水平力F=10N 拉物体由A点开始运动,经过8s后撤去拉力F,再经过一段时间物体到达B点停止.(g=10m/s2)求:
(1)在拉力F作用下物体运动的加速度多大?
(2)撤去F后物体运动的距离多大?运动时间多长?
(3)画出物体整个运动过程的速度-时间图象.
解:(1)加速时,物体受重力、拉力、支持力和摩擦力四个力的作用,由牛顿第二定律:
F-μmg=ma
1 解得:a
1=0.5m/s
2 (2)加速过程中由运动学公式得 v=a
1t
1=4m/s,
撤去F后 a
2=-μg=-2 m/s
2 由 2a
2x
2=0-v
2 所以 x
2=4m,
由速度公式可得 0-v=a
2t
2 所以 t
2=2s.
(3)由(1)(2)的分析可知,物体的初速度为0,做匀加速运动,经8s,速度达到=4m/s,

之后开始匀减速运动,经2s,速度减为0.所以速度-时间图象如图所示.
答:(1)在拉力F作用下物体运动的加速度0.5m/s
2,
(2)撤去F后物体运动的距离是4m,时间是2s,
(3)整个运动过程的速度-时间图象如图所示.
分析:(1)分析物体的运动过程可知,物体先做加速度运动,由牛顿第二定律可以求得加速度的大小,
(2)撤掉拉力后再做减速运动,根据牛顿第二定律求得加速度,再根据匀变速直线运动的规律求得位移和时间,
(3)根据整体的运动情况可以画出速度-时间图象.
点评:由牛顿第二定律求得加速度后,利用匀变速直线运动的规律求解即可,本题主要就是匀变速直线运动规律的应用,题目较简单.




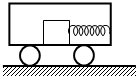 如图所示,小车以2m/s2的加速度水平向右做匀减速运动.其光滑底面上有一质量为4kg的物体.一轻弹簧其两端分别固定在车厢右侧和物体上.它们都相对于车厢静止.则( )
如图所示,小车以2m/s2的加速度水平向右做匀减速运动.其光滑底面上有一质量为4kg的物体.一轻弹簧其两端分别固定在车厢右侧和物体上.它们都相对于车厢静止.则( )