在香港海洋公园的游乐场中,有一台大型游戏机叫“跳楼机”.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处,然后由静止释放.座椅沿轨道自由下落一段时间后,开始受到压缩空气提供的恒定阻力而紧接着做匀减速运动,下落到离地面4.0m高处速度刚好减小到零,这一下落全过程经历的时间是6s.求:(取g=10m/s2)
(1)座椅被释放后做自由下落的末速度v
(2)座椅被释放后做自由下落的高度h
(3)在匀减速运动阶段,座椅的加速度大小是多少.
解:(1)画出v-t图,

由图象知,
“面积”s=

vt,
得到v=
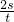
=
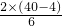
m/s=12 m/s
(2)根据自由落体运动规律,
座椅被释放后自由下落的高度
h=

=
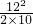
m=7.2 m.
(3)物体做匀减速运动的位移
s′=(36-7.2)m=28.8 m,
由公式v
2=2as′可知
在匀减速运动阶段,
游客的加速度大小
a=
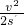
=
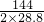
m/s
2=2.5 m/s
2.
答:(1)座椅被释放后做自由下落的末速度v为12 m/s;
(2)座椅被释放后做自由下落的高度h为7.2 m;
(3)在匀减速运动阶段,座椅的加速度大小是2.5 m/s
2.
分析:(1)分析座椅的运动情况,先做自由落体运动,然后做匀减速直线运动直到静止,画出速度-时间图象,根据图象与时间轴围成的面积表示位移即可解题;
(2)求出自由下落的末速度v后,根据位移-速度公式即可求得自由下落的高度h;
(3)先物体做匀减速运动的位移,再根据匀减速直线运动位移-速度公式即可解题.
点评:该题主要考查了自由落体运动和匀减速直线运动位移-时间公式的直接应用,有时利用图象等其它方法解题比较简单,难度不大.


 vt,
vt,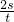 =
=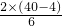 m/s=12 m/s
m/s=12 m/s =
=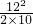 m=7.2 m.
m=7.2 m.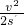 =
=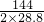 m/s2=2.5 m/s2.
m/s2=2.5 m/s2.

 阅读快车系列答案
阅读快车系列答案