

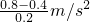 =2m/s2,
=2m/s2,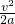 =0.08m
=0.08m  a2t2=0.16m
a2t2=0.16m 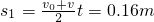
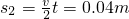


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:
 如图所示,一质量M=50kg、长L=3m的平板车静止在光滑的水平地面上,平板车上表面距地面的高度h=1.8m.一质量m=10kg可视为质点的滑块,以v0=7.5m/s的初速度从左端滑上平板车,滑块与平板车间的动摩擦因数μ=0.5,取g=10m/s2.
如图所示,一质量M=50kg、长L=3m的平板车静止在光滑的水平地面上,平板车上表面距地面的高度h=1.8m.一质量m=10kg可视为质点的滑块,以v0=7.5m/s的初速度从左端滑上平板车,滑块与平板车间的动摩擦因数μ=0.5,取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,一质量M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一质量m=1.0kg的小木块A,现以地面为参照系,给A和B以大小均为4.0m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,最后A相对B静止,此时A的速度为( )
如图所示,一质量M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一质量m=1.0kg的小木块A,现以地面为参照系,给A和B以大小均为4.0m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,最后A相对B静止,此时A的速度为( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,一质量M=2kg的斜面体静止在水平地面上,斜面体与地面间的动摩擦因数为μ=0.5,斜面夹角α=37°.一质量m=1kg的光滑小球放在斜面体与竖直墙壁之间,处于静止状态.若在光滑小球的正上方施加一个竖直向下的力,要使斜面体向右移动,竖直向下的力F至少为多大?(设滑动摩擦力等于最大静摩擦力,g取10m/s2)
如图所示,一质量M=2kg的斜面体静止在水平地面上,斜面体与地面间的动摩擦因数为μ=0.5,斜面夹角α=37°.一质量m=1kg的光滑小球放在斜面体与竖直墙壁之间,处于静止状态.若在光滑小球的正上方施加一个竖直向下的力,要使斜面体向右移动,竖直向下的力F至少为多大?(设滑动摩擦力等于最大静摩擦力,g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
 (2011?湖南模拟)如图所示,一质量M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一个质量m=1.0kg的小木块A.现以地面为参考系,给A和B大小均为4.0m/s方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A静止在B板上一起运动,则这一过程中下列哪些物理量可求( )
(2011?湖南模拟)如图所示,一质量M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一个质量m=1.0kg的小木块A.现以地面为参考系,给A和B大小均为4.0m/s方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A静止在B板上一起运动,则这一过程中下列哪些物理量可求( )查看答案和解析>>
科目:高中物理 来源: 题型:
 (2011?太原模拟)如图所示,一质量m=65kg的选手参加“挑战极限运动”,要在越过宽度s=3m的水沟后跃上高h=1.8m的平台.他采用的方法是:手握长L=3.05m的轻质弹性杆一端,从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直(不弯曲),人的重心恰好位于杆的顶端,此刻人放开杆水平飞出,最终落到平台上(重心恰在平台表面).不计运动过程中的空气阻力,取g=10m/s2:
(2011?太原模拟)如图所示,一质量m=65kg的选手参加“挑战极限运动”,要在越过宽度s=3m的水沟后跃上高h=1.8m的平台.他采用的方法是:手握长L=3.05m的轻质弹性杆一端,从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直(不弯曲),人的重心恰好位于杆的顶端,此刻人放开杆水平飞出,最终落到平台上(重心恰在平台表面).不计运动过程中的空气阻力,取g=10m/s2:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com