
解法一 公式法
从竖直上抛运动的整个过程来看,小球作可往返的匀减速直线运动,设第二个小球抛出后经时间t与第一个小球相遇,两球相遇时其位移相等,由公式
s=v0t-gt2/ 2有
20(t+1)-g(t+1)2/ 2=20t-gt2/ 2
整理得 15-gt=0
则 t=1.5s.
解法二 “速率对称法”
在竖直上抛运动的过程中,在同一高度处,物体上升与下降的速率相等,即两球相遇时的速度大小相等,方向相反,则有
-[20-g(t+1)]=20-gt
则 t=1.5s.
解法三 “时间对称法”
在竖直上抛运动过程中,物体从某高度处到达最高点的时间与从最高点返回到该处的时间相等.则两球运动过程如图1所示.由于第一个小球比第二个小球提前 1s抛出,则可知第一个小球从相遇处到最高点和从最高点到相遇处的时间分别为0.5s.
则 t′=v0/g=20/10=2s
而t′=t+0.5s,故t=1.5s.
解法四 逆向分析法
在竖直上抛运动过程中,物体下落是物体上升的逆过程,因此,第二个小球上升t时的速率应等于第一个小球从最高点下落0.5s时的速率,则0.5×g=20-gt,故t=1.5s.
解法五 相对运动法
当第二个小球抛出时,第一个小球的速度v=v0-gΔt=20-10×1=10m/s,上升的距离s=v×Δt=15m,若以第一个小球为参照物,则第二个小球以速度v′=10m/s向上做匀速运动,设第二个小球抛出后经时间t两球相遇,第二个小球相对于第一个小球运动的距离s′=v′t=15m,故t=1.5s.
解法六 速度图象法

在同一个坐标系中画出两个小球运动的速度与时间的图象如图2所示,在相遇时,两球的位移相等,则有梯形HKEF与梯形AONB的面积相等.即SHKEF=SAOC-SBMC.
而
则可得 20-5(t-1)2=5t(t+1)
整理得 2t2-t-3=0,(2t-3)(t+1)=0
t1=1.5s,t2=-1s(舍去)
解法七 位移图象法
在同一个坐标系中画出两个小球运动的位移与时间的图象如图3所示,两位移图象的交点表示在该时刻两球的位移相等.即两小球在该时刻相遇.由对称性可知交点的横坐标t=2.5s,则可知第二个小球抛出后经过1.5s与第一个小球相遇.


科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
如图所示,图线I和Ⅱ分别表示先后从同一地点以相同速度v作竖直上抛运动的两物体的v-t图线,则两物体
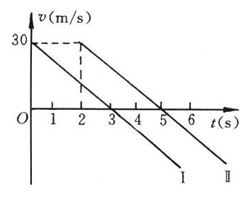
A.在第Ⅰ个物体抛出后3s末相遇
B.在第Ⅱ个物体抛出后4s末相遇
C.在第Ⅱ个物体抛出后2s末相遇
D.相遇时必有一个物体速度为零
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com