
 如图所示,ABC为光滑轨道,其中AB段水平放置,BC段是半径为R的圆弧,AB与BC相切于B点.A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧牌原长状态时,物块恰能与固定在墙上的L形挡板相接触于B处但无挤压.现使一质量为m的小球从圆孤轨道上距水平轨道高h处的D点由静止开始下滑,小球与物块相碰后立即共速但不粘连,物块与L形挡板相碰后速度立即减为零也不粘连.(整个过程中,弹簧没有超过弹性限度,不计空气阻力,重力加速度为g)
如图所示,ABC为光滑轨道,其中AB段水平放置,BC段是半径为R的圆弧,AB与BC相切于B点.A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧牌原长状态时,物块恰能与固定在墙上的L形挡板相接触于B处但无挤压.现使一质量为m的小球从圆孤轨道上距水平轨道高h处的D点由静止开始下滑,小球与物块相碰后立即共速但不粘连,物块与L形挡板相碰后速度立即减为零也不粘连.(整个过程中,弹簧没有超过弹性限度,不计空气阻力,重力加速度为g)
|
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| m2gh |
| M+m |
| 1 |
| 2 |
| v | 2 1 |
| m2 |
| (M+m)2 |
|
| 3 |
| 4 |
| 3 |
| 2 |
|
| m2gh |
| M+m |
| m2 |
| (M+m)2 |
| 3 |
| 2 |
|


科目:高中物理 来源: 题型:
 (2013?永州一模)如图所示,ABC为某种透明介质的横截面图,其中△AOC为等腰直角三角形,BC为半径R=10cm的四分之一圆弧,AB与水平屏幕MN垂直并接触于A点.由红光和紫光两种单色光组成的复色光经过BC面射向圆心O,在AB分界面上的入射角i=45°,结果在水平屏幕MN上出现两个亮斑,已知该介质对红光和紫光的折射率分别为n1=
(2013?永州一模)如图所示,ABC为某种透明介质的横截面图,其中△AOC为等腰直角三角形,BC为半径R=10cm的四分之一圆弧,AB与水平屏幕MN垂直并接触于A点.由红光和紫光两种单色光组成的复色光经过BC面射向圆心O,在AB分界面上的入射角i=45°,结果在水平屏幕MN上出现两个亮斑,已知该介质对红光和紫光的折射率分别为n1=2
| ||
| 3 |
| 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏.一束宽度等于AB的单色平行光束垂直射向AB面,经三棱镜折射后在屏P上形成一条光带.
如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏.一束宽度等于AB的单色平行光束垂直射向AB面,经三棱镜折射后在屏P上形成一条光带.查看答案和解析>>
科目:高中物理 来源: 题型:
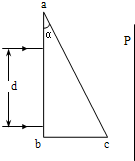 如图所示,△abc为一直角三棱镜的横截面,其顶角α=30°,P是平行于ab的光屏.现有一束宽度为d的单色平行光垂直射向ab面,结果在屏P上形成一宽度等于
如图所示,△abc为一直角三棱镜的横截面,其顶角α=30°,P是平行于ab的光屏.现有一束宽度为d的单色平行光垂直射向ab面,结果在屏P上形成一宽度等于| 2 | 3 |
查看答案和解析>>
科目:高中物理 来源: 题型:
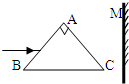 如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )
如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )| A、BC面将有色光射出 | B、光屏M上会出现色彩光带且紫光在上 | C、光屏M上会出现色彩光带且红光在上 | D、将光屏保持与BC垂直向右平移,屏上彩色光带宽度不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:
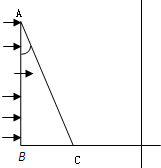 如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为
如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为| 2 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com