
 数形结合能力是高考能力要求之一,图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,图乙为质点Q的振动图象,则下列判断错误的( )
数形结合能力是高考能力要求之一,图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,图乙为质点Q的振动图象,则下列判断错误的( )| 1 |
| T |
| 8 |
| 0.2 |
| 3 |
| 4 |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中物理 来源: 题型:
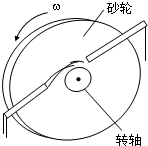 探究能力是物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系.某同学采用了下述实验方法进行探索:如图先让砂轮由动力带动匀速旋转测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据,得出结论.经实验测得的几组ω和n如下表所示:
探究能力是物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系.某同学采用了下述实验方法进行探索:如图先让砂轮由动力带动匀速旋转测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据,得出结论.经实验测得的几组ω和n如下表所示:| ω/rad?s-1 | 0.5 | 1 | 2 | 3 | 4 |
| n | 5.0 | 20 | 80 | 180 | 320 |
| Ek/J |
查看答案和解析>>
科目:高中物理 来源: 题型:
| 10 |
| π |
| 半径r/cm | 质量/m0 | 角速度(rad/s) | 圈数 | 转动动能/J |
| 4 | 1 | 2 | 8 | |
| 4 | 1 | 3 | 18 | |
| 4 | 1 | 4 | 32 | |
| 4 | 2 | 2 | 16 | |
| 4 | 3 | 2 | 24 | |
| 4 | 4 | 2 | 32 | |
| 8 | 1 | 2 | 16 | |
| 12 | 1 | 2 | 24 | |
| 16 | 1 | 2 | 32 |
查看答案和解析>>
科目:高中物理 来源: 题型:
数形结合能力是高考能力要求之一,图甲为一列简谐横波在![]() 时刻的波形图,
时刻的波形图,![]() 是平衡位置为
是平衡位置为![]() 处的质点,
处的质点,![]() 是平衡位置为
是平衡位置为![]() 处的质点,图乙为质点
处的质点,图乙为质点![]() 的振动图像,则下列判断错误的
的振动图像,则下列判断错误的

A.该简谐横波的传播方向沿x轴的正方向
B.![]() 时,质点
时,质点![]() 的加速度达到正向最大
的加速度达到正向最大
C.![]() 时,质点
时,质点![]() 的运动方向沿
的运动方向沿![]() 轴负方向
轴负方向
D.![]() 到
到![]() ,质点
,质点![]() 通过的路程为
通过的路程为![]()
查看答案和解析>>
科目:高中物理 来源:同步题 题型:不定项选择
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com