
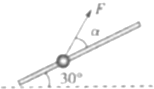
 如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )
如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )| A. | 当α=30°时,拉力F最小 | B. | 当α=30°时,拉力F做功最小 | ||
| C. | 当α=60°时,拉力F最小 | D. | 当α=60°时,拉力F做功最小 |
分析 对小球受力分析,根据受力平衡列方程,然后结合数学三角函数知识求F的最小值,解本题的突破口为找到使拉力做功最小的条件,为此要分析小球受到的各个力及做功情况:重力做负功,弹力不做功,拉力F做正功,又因小球做匀速运动,动能的变化为零,那么只要摩擦力不做功(即摩擦力为零),则拉力F做功最小,然后正交分解小球受到的各力,列力的平衡方程解答即可求出答案.
解答 解:小球匀速运动,根据平衡条件,在沿杆方向上有:
Fcosα=mgsin30°+μ(mgcos30°-Fsinα)
整理得:Fcosα+μFsinα=10
F=$\frac{1}{cosα+μsinα}$•mg
由数学知识知当cosα+μsinα最大值为$\sqrt{{1}^{2}+(\frac{\sqrt{3}}{3})^{2}}=\frac{2}{\sqrt{3}}$
此时arctan$\frac{1}{μ}$=60° 则α=90°-60°=30°,故A正确,C错误;
B、小球匀速运动,由动能定理得;WF-Wf-WG=0
要使拉力做功最小则Wf=0,即摩擦力为0,则支持力为0.
分析小球受的各力然后正交分解列方程:
垂直斜面方向:Fsinα=mgcos30°
沿斜面方向:Fcosα=mgsin30°
解以上两方程得:α=60°,F=mg,故B错误,D正确;
故选:AD
点评 本题考查了受力分析以及正交分解的应用,关键是熟练结合数学知识求极值.通过分析小球的受力及各力做功情况,再结合动能定理得出拉力F做功最小时摩擦力为零.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
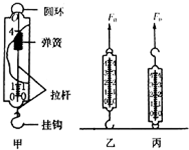 实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )| A. | 乙图读数F0-G,丙图读数F0+G | B. | 乙图读数F0+G,丙图读数F0-G | ||
| C. | 乙图读数F0,丙图读数F0-G | D. | 乙图读数F0-G,丙图读数F0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在验证动量守恒的实验中:
如图所示,在验证动量守恒的实验中:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 是a=g的匀变速运动 | |
| B. | 可分解为竖直向上的匀速直线运动和自由落体运动 | |
| C. | 可以把从最高点下落的后半段运动看作是自由落体运动 | |
| D. | 上升过程的加速度小于下落过程的加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
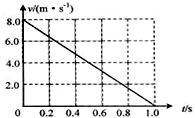 一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的v-t图线,如图所示.(取sin 37°=0.6,cos 37°=0.8,g=10m/s2)求:
一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的v-t图线,如图所示.(取sin 37°=0.6,cos 37°=0.8,g=10m/s2)求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com