
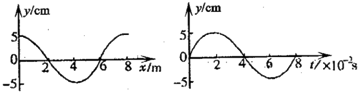
 一列沿x轴传播的横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.求:
一列沿x轴传播的横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.求:| s |
| t |
| 1 |
| 4 |
| s |
| t |
| 8n+2 |
| 0.005 |
| 3 |
| 4 |
| s |
| t |
| 8n+6 |
| 0.005 |
| s |
| λ |
| 18 |
| 8 |
| 1 |
| 4 |


科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
一列沿x轴传播的横波在某一时刻的波形图象如图12-2-12所示,已知波的传播速率是16 m/s,且该时刻P质点沿y轴正方向运动。

图12-2-12
(1)指出这列波的传播方向。
(2)图示时刻Q质点与P质点的位移相同,那么下一时刻它们的位移还相等吗?Q点的速度将如何变化?
(3)画出再经过0.125 s时的波形图象。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com