
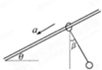
 如图所示,一固定光滑杆与水平方向夹角为θ,将一质量为m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,小环与小球保持相对静止以相同的加速度a一起下滑,此时绳子与竖直方向夹角为β,则下列说法正确的是
如图所示,一固定光滑杆与水平方向夹角为θ,将一质量为m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,小环与小球保持相对静止以相同的加速度a一起下滑,此时绳子与竖直方向夹角为β,则下列说法正确的是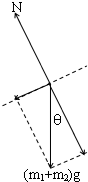 解:A、以整体为研究对象,分析受力情况,如图,
解:A、以整体为研究对象,分析受力情况,如图,

科目:高中物理 来源: 题型:
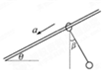 如图所示,一固定光滑杆与水平方向夹角为θ,将一质量为m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,小环与小球保持相对静止以相同的加速度a一起下滑,此时绳子与竖直方向夹角为β,则下列说法正确的是( )
如图所示,一固定光滑杆与水平方向夹角为θ,将一质量为m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,小环与小球保持相对静止以相同的加速度a一起下滑,此时绳子与竖直方向夹角为β,则下列说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
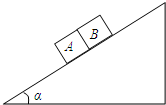 如图所示,一固定斜面上的两个小物块A和B紧挨着匀速下滑,A和B的质量分别为mA=1kg,mB=2kg且A与B的接触面光滑,已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角α=37°,求:
如图所示,一固定斜面上的两个小物块A和B紧挨着匀速下滑,A和B的质量分别为mA=1kg,mB=2kg且A与B的接触面光滑,已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角α=37°,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 (2006?福建模拟)如图所示,一固定在地面上的光滑斜面的顶端固定有一个轻弹簧,地面上质量为m的物块(可视为质点)向右滑行并冲上斜面,设物块在斜面最低点A的速率为υ,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则物块运动到C点时弹簧的弹性势能为( )
(2006?福建模拟)如图所示,一固定在地面上的光滑斜面的顶端固定有一个轻弹簧,地面上质量为m的物块(可视为质点)向右滑行并冲上斜面,设物块在斜面最低点A的速率为υ,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则物块运动到C点时弹簧的弹性势能为( )查看答案和解析>>
科目:高中物理 来源: 题型:
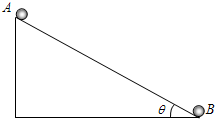 如图所示,一固定的光滑斜面倾角为θ=30°,斜面长为L.从斜面顶端无初速释放一质量为m的小球A,同时另一质量为m的小球B从斜面底端以某一初速度沿斜面向上运动,已知两球都可看成质点,碰撞为正碰且碰撞时无机械能损失,重力加速度为g.问:
如图所示,一固定的光滑斜面倾角为θ=30°,斜面长为L.从斜面顶端无初速释放一质量为m的小球A,同时另一质量为m的小球B从斜面底端以某一初速度沿斜面向上运动,已知两球都可看成质点,碰撞为正碰且碰撞时无机械能损失,重力加速度为g.问:查看答案和解析>>
科目:高中物理 来源:0103 期末题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com