
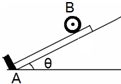
 电动机带动滚轮匀速转动,在滚轮的作用下,将金属杆从最底端A送往倾角θ=30°的足够长斜面上部.滚轮中心B与斜面底部A的距离为L=6.5m,当金属杆的下端运动到B处时,滚轮提起,与杆脱离接触.杆由于自身重力作用最终会返回斜面底部,与挡板相撞后,立即静止不动.此时滚轮再次压紧杆,又将金属杆从最底端送往斜面上部,如此周而复始.已知滚轮边缘线速度恒为v=4m/s,滚轮对杆的正压力FN=2×104N,滚轮与杆间的动摩擦因数为μ=0.35,杆的质量为m=1×103Kg,不计杆与斜面间的摩擦,取g=10m/s2.求:
电动机带动滚轮匀速转动,在滚轮的作用下,将金属杆从最底端A送往倾角θ=30°的足够长斜面上部.滚轮中心B与斜面底部A的距离为L=6.5m,当金属杆的下端运动到B处时,滚轮提起,与杆脱离接触.杆由于自身重力作用最终会返回斜面底部,与挡板相撞后,立即静止不动.此时滚轮再次压紧杆,又将金属杆从最底端送往斜面上部,如此周而复始.已知滚轮边缘线速度恒为v=4m/s,滚轮对杆的正压力FN=2×104N,滚轮与杆间的动摩擦因数为μ=0.35,杆的质量为m=1×103Kg,不计杆与斜面间的摩擦,取g=10m/s2.求:| f-mgsinθ |
| m |
| v |
| a |
| 4 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中物理 来源: 题型:阅读理解
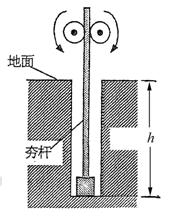
如图所示,建筑工地常用的一种“深穴打夯机”工作时,电动机带动两个紧压夯杆的滚轮匀速转动将夯从深为h的坑中提到地面,两个滚轮彼此分开,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底,然后,两个滚轮再次压紧夯杆,夯再次被提到地面,如此周而复始。已知两个滚轮的半径R=0.2m,转动的角速度![]() ,每个滚轮对夯杆的正压力
,每个滚轮对夯杆的正压力![]() ,滚轮与夯杆间的动摩擦因数
,滚轮与夯杆间的动摩擦因数![]() ,夯的总质量
,夯的总质量![]() kg,坑深h=6.4m,假定在打夯的过程中每次坑的深度变化不大,当夯的底端升到坑口时,滚轮将夯杆释放,不计空气阻力,取g=10m/s2,求:
kg,坑深h=6.4m,假定在打夯的过程中每次坑的深度变化不大,当夯的底端升到坑口时,滚轮将夯杆释放,不计空气阻力,取g=10m/s2,求:
(1)夯杆被滚轮压紧加速上升至与滚轮速度相等时,此时夯的底端离坑底的高度h1;
(2)夯的运动周期T;
(3)每个周期中,提升夯的过程中电动机所做的功W.
将1molCO和1molH2O充入某固定容积的反应器中,在某条件下达到平衡:
CO+H2O(g)![]() CO2+H2,此时有2/3的CO转化为CO2。
CO2+H2,此时有2/3的CO转化为CO2。
(1)该平衡混合物中CO2的体积分数为
(2)若容器体积为1L,到达平衡所需时间为2分钟,则H2的平均反应速率为
(3)若在相同条件下,向容器中充入1molCO2、1molH2和1molH2O,则达到平衡时与⑴中平衡相比较,平衡应向 (填“正反应方向”、“逆反应方向”或“不”)移动,此时平衡混合物中CO2的体积分数可能是下列各值中的
A.22.2% B.27.55% C.33.3% D.36.8%
(4)结合(3)中计算结果分析若平衡向正方向移动时,则下列说法中正确的是( )
①生成物的产量一定增加; ②生成物的体积分数一定增加;
③反应物的转化率一定增大; ④反应物的浓度一定降低;
⑤正反应速率一定大于逆反应速率; ⑥一定使用了催化剂.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com