
 a1t2
a1t2 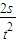 =
=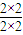 m/s2=1 m/s2
m/s2=1 m/s2 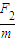 =2 m/s2
=2 m/s2  a1t2=(-2-2×2+
a1t2=(-2-2×2+ ×1×22)m=-4 m
×1×22)m=-4 m  a2t2=-
a2t2=- ×2×22 m=-4 m
×2×22 m=-4 m 

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中物理 来源: 题型:
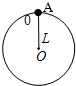 长度为L=0.4m的轻质细杆OA,A端连有一质量为m=2kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是1m/s,则此时细杆对小球的作用力为( )
长度为L=0.4m的轻质细杆OA,A端连有一质量为m=2kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是1m/s,则此时细杆对小球的作用力为( )查看答案和解析>>
科目:高中物理 来源: 题型:
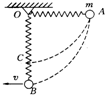 如图所示,质量为m=2kg的小球系在轻质弹簧的一端,另一端固定在悬点O处,将弹簧拉至水平位置A处,且弹簧处于自然状态,弹簧的原长0A=0.3m;然后小球由静止释放,小球到达距O点下方h=0.5m处的B点时速度为VB=2m/s,求
如图所示,质量为m=2kg的小球系在轻质弹簧的一端,另一端固定在悬点O处,将弹簧拉至水平位置A处,且弹簧处于自然状态,弹簧的原长0A=0.3m;然后小球由静止释放,小球到达距O点下方h=0.5m处的B点时速度为VB=2m/s,求查看答案和解析>>
科目:高中物理 来源: 题型:
 处于静止状态.两车之间有一感应机关,在它的作用下,当滑块滑过两车连接处时,两车将自动分离.现剪断细线,滑块先后在甲、乙小车上滑行,最终滑块恰好滑到乙车的另一端而未滑出乙车.取g=10m/s2,求:
处于静止状态.两车之间有一感应机关,在它的作用下,当滑块滑过两车连接处时,两车将自动分离.现剪断细线,滑块先后在甲、乙小车上滑行,最终滑块恰好滑到乙车的另一端而未滑出乙车.取g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,一辆质量为M=6kg的小车静止在光滑的水平面上,另一质量为m=2kg的物块(可视为质点)静止在小车上的A点;在物块和小车右侧的挡板之间夹有一被压缩的轻质弹簧(弹簧和物块不相连),弹簧的弹性势能为4J,物块和挡板之间用细线连结.已知物块和小车之间的动摩擦因数μ=0.2.某时刻将细线烧断,弹簧将物块弹开,最后物块停在小车上的B点,取g=10m/s2.
如图所示,一辆质量为M=6kg的小车静止在光滑的水平面上,另一质量为m=2kg的物块(可视为质点)静止在小车上的A点;在物块和小车右侧的挡板之间夹有一被压缩的轻质弹簧(弹簧和物块不相连),弹簧的弹性势能为4J,物块和挡板之间用细线连结.已知物块和小车之间的动摩擦因数μ=0.2.某时刻将细线烧断,弹簧将物块弹开,最后物块停在小车上的B点,取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:
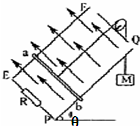 如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求:
如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com