
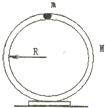
 一附有底座得内壁光滑得环形细圆管,质量为M,位于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有一个直径略小于细管内径得小球(刻视为质点),球得质量为m,它沿环形圆管顺时针运动,环形圆管始终静止在地面上,小球经过最低点时得速度为v2.当小球运动到最高点时,圆管对地面得作用力为零,那么m、M、R与v2应满足什么关系?
一附有底座得内壁光滑得环形细圆管,质量为M,位于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有一个直径略小于细管内径得小球(刻视为质点),球得质量为m,它沿环形圆管顺时针运动,环形圆管始终静止在地面上,小球经过最低点时得速度为v2.当小球运动到最高点时,圆管对地面得作用力为零,那么m、M、R与v2应满足什么关系?| v2 |
| R |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
| v | 2 0 |
| v | 2 0 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com