
分析 研究飞船绕星球做匀速圆周运动,根据万有引力提供向心力,列出等式求出中心体的质量;研究登陆舱绕星球做匀速圆周运动,根据万有引力提供向心力,列出等式表示出线速度和周期;再通过不同的轨道半径进行比较.
解答 解:(1)研究飞船绕星球做匀速圆周运动,
根据万有引力提供向心力,列出等式:$G\frac{M{m}_{1}}{{{r}_{1}}^{2}}={m}_{1}{r}_{1}\frac{4{π}^{2}}{{{T}_{1}}^{2}}$,
解得:M=$\frac{4{π}^{2}{{r}_{1}}^{3}}{G{{T}_{1}}^{2}}$.
(2)研究登陆舱绕星球做匀速圆周运动,根据万有引力提供向心力$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$,
在半径为r的圆轨道上运动:$v=\sqrt{\frac{GM}{R}}$,表达式里M为中心体星球的质量,R为运动的轨道半径;
所以登陆舱在r1与r2轨道上运动时的速度大小之比为:$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$
(3)研究登陆舱绕星球做匀速圆周运动,
根据万有引力提供向心力$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}R$,得出:T=2π$\sqrt{\frac{{R}^{3}}{GM}}$;
表达式里M为中心体星球的质量,R为运动的轨道半径.
所以登陆舱在r1与r2轨道上运动时的周期大小之比为$\sqrt{\frac{{{r}_{1}}^{3}}{{{r}_{2}}^{3}}}$,所以周期为T2=T1$\sqrt{\frac{{{r}_{1}}^{3}}{{{r}_{2}}^{3}}}$;
答:(1)X星球的质量为$\frac{4{π}^{2}{{r}_{1}}^{3}}{G{{T}_{1}}^{2}}$;
(2)登陆舱在r1与r2轨道上运动的速度大小之比为$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$;
(3)登陆舱在半径为r2轨道上做圆周运动的周期为T1$\sqrt{\frac{{{r}_{1}}^{3}}{{{r}_{2}}^{3}}}$.
点评 本题主要考查万有引力提供向心力这个关系,要注意向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.


科目:高中物理 来源: 题型:选择题
| A. | 刹车前的行驶速度为10m/s | B. | 刹车过程中的加速度为2m/s2 | ||
| C. | 刹车后的行驶时间为10s | D. | 刹车后的位移为50m |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
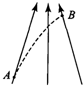 如图所示,带箭头的线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )
如图所示,带箭头的线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )| A. | 粒子带负电 | B. | 粒子在A点加速度大 | ||
| C. | 粒子在B点动能大 | D. | A、B两点相比,B点电势能较高 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{F}_{1}}{{F}_{2}}$ | B. | $\frac{{F}_{2}}{{F}_{1}}$ | C. | $\sqrt{\frac{{F}_{1}}{{F}_{2}}}$ | D. | $\sqrt{\frac{{F}_{2}}{{F}_{1}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
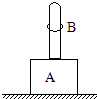 如图底座A上装有长0.5m的直立杆,其总质量M=0.2kg,杆上套有质量m=0.05kg的小环B,它与杆之间有大小恒定的摩擦力.当环从底座上以4m/s的速度飞起时刚好能到达杆顶,求(g取10m/s2):
如图底座A上装有长0.5m的直立杆,其总质量M=0.2kg,杆上套有质量m=0.05kg的小环B,它与杆之间有大小恒定的摩擦力.当环从底座上以4m/s的速度飞起时刚好能到达杆顶,求(g取10m/s2):查看答案和解析>>
科目:高中物理 来源: 题型:选择题
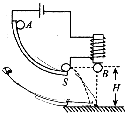 如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两个小球总是同时落地,该实验现象说明了A球在离开轨道后( )
如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两个小球总是同时落地,该实验现象说明了A球在离开轨道后( )| A. | 竖直方向的分运动是匀速直线运动 | |
| B. | 竖直方向的分运动是自由落体运动 | |
| C. | 水平方向的分运动是匀加速直线运动 | |
| D. | 水平方向的分运动是匀速直线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 经过任意两个连续相等的距离的时间之差为常数 | |
| B. | 在相邻且相等的时间间隔内的位移之差为最初的那个时间间隔内的位移的两倍 | |
| C. | 在运动过程中,任意两个相等的时间间隔内速度的改变量相同 | |
| D. | 在运动过程中,任意两个相等的时间间隔内位移的大小之比一定是奇数 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com