
 如图,一足够长的平木板静置于水平地面上,质量为M=4kg,从某时刻开始给木板施加一水平向右的大小为20N的恒力F,使木板开始运动,经过3秒时,在木板的前端轻放一个初速度为0质量为m=4kg的小物块.已知物块与木板的摩擦因数为μ1=0.1,木板与地面间的摩擦因数为μ2=0.4,静摩擦因数和动摩擦因数相同,重力加速度g=10m/s2.试求:
如图,一足够长的平木板静置于水平地面上,质量为M=4kg,从某时刻开始给木板施加一水平向右的大小为20N的恒力F,使木板开始运动,经过3秒时,在木板的前端轻放一个初速度为0质量为m=4kg的小物块.已知物块与木板的摩擦因数为μ1=0.1,木板与地面间的摩擦因数为μ2=0.4,静摩擦因数和动摩擦因数相同,重力加速度g=10m/s2.试求: =1m/s2
=1m/s2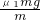 =1m/s2
=1m/s2 =4m/s2
=4m/s2 a1t12=0.18m
a1t12=0.18m a2t12=1.08m
a2t12=1.08m =2m/s2
=2m/s2  a1?t22=0.135m
a1?t22=0.135m a2?t22=0.09m
a2?t22=0.09m =0.045m
=0.045m 

 步步高达标卷系列答案
步步高达标卷系列答案科目:高中物理 来源: 题型:
 如图,一足够长的平木板静置于水平地面上,质量为M=4kg,从某时刻开始给木板施加一水平向右的大小为20N的恒力F,使木板开始运动,经过3秒时,在木板的前端轻放一个初速度为0质量为m=4kg的小物块.已知物块与木板的摩擦因数为μ1=0.1,木板与地面间的摩擦因数为μ2=0.4,静摩擦因数和动摩擦因数相同,重力加速度g=10m/s2.试求:
如图,一足够长的平木板静置于水平地面上,质量为M=4kg,从某时刻开始给木板施加一水平向右的大小为20N的恒力F,使木板开始运动,经过3秒时,在木板的前端轻放一个初速度为0质量为m=4kg的小物块.已知物块与木板的摩擦因数为μ1=0.1,木板与地面间的摩擦因数为μ2=0.4,静摩擦因数和动摩擦因数相同,重力加速度g=10m/s2.试求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图,一足够长的固定斜面与水平方向成α=37?角,空间有垂直于斜面的无限多个匀强磁场,其磁感应强度的大小均为B=0.5T,相邻磁场区域的磁场方向相反.每个磁场区域的宽度均为L1=0.1m,磁场区的边界均与斜面底边平行.现有一质量为m=0.05kg、电阻为R=0.5Ω的矩形金属框abcd沿此斜面下滑,已知ad=L1=0.1m,ab=L2=0.2m,下滑过程中,金属框的ab边始终与斜面底边平行,金属框与斜面间的动摩擦因数为μ=0.2,金属框下滑距离s=3m时速度达到最大,求:
如图,一足够长的固定斜面与水平方向成α=37?角,空间有垂直于斜面的无限多个匀强磁场,其磁感应强度的大小均为B=0.5T,相邻磁场区域的磁场方向相反.每个磁场区域的宽度均为L1=0.1m,磁场区的边界均与斜面底边平行.现有一质量为m=0.05kg、电阻为R=0.5Ω的矩形金属框abcd沿此斜面下滑,已知ad=L1=0.1m,ab=L2=0.2m,下滑过程中,金属框的ab边始终与斜面底边平行,金属框与斜面间的动摩擦因数为μ=0.2,金属框下滑距离s=3m时速度达到最大,求:查看答案和解析>>
科目:高中物理 来源:2009-2010学年湖北省荆州中学高三(上)月考物理试卷(9月份)(解析版) 题型:解答题

查看答案和解析>>
科目:高中物理 来源:2010-2011学年福建省厦门市思明区双十中学高三(下)开学初物理试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com