
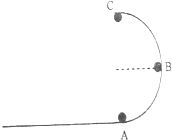
 如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m,质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点,与圆心等高点、最高点.小球过这三点的速度分别为:v1=5m/s,v2=4m/s,v3=3m/s,求:
如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m,质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点,与圆心等高点、最高点.小球过这三点的速度分别为:v1=5m/s,v2=4m/s,v3=3m/s,求:分析 (1)在A、C两点,小球靠重力和弹力的合力提供向心力,在B点,小球靠弹力提供向心力,结合牛顿第二定律求出轨道对小球的弹力大小,从而结合牛顿第三定律得出小球经过这三个位置时对轨道的压力;
(2)根据高度求出平抛运动的时间,结合C点的速度和时间求出着地点与A点的距离;
(3)当小球到达最高点,刚好由重力提供向心力时,速度最小,根据牛顿第二定律求解最小速度.
解答 解:(1)在A点,根据牛顿第二定律得:${N}_{A}-mg=m\frac{{{v}_{A}}^{2}}{R}$,
解得:${N}_{A}=mg+m\frac{{{v}_{A}}^{2}}{R}$=2+0.2×$\frac{25}{0.2}$N=27N.
在B点,根据牛顿第二定律得:${N}_{B}=m\frac{{{v}_{B}}^{2}}{R}=0.2×\frac{16}{0.2}$N=16N.
在C点,根据牛顿第二定律得:${N}_{C}-mg=m\frac{{{v}_{C}}^{2}}{R}$,
解得:${N}_{C}=m\frac{{{v}_{C}}^{2}}{R}-mg=0.2×\frac{9}{0.2}-2$=7N,
根据牛顿第三定律知,小球经过三个位置时对轨道的压力分别为27N、16N、7N.
(2)根据2R=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{4R}{g}}$,
着地点与A点相距为:x=${v}_{C}t=3×\sqrt{\frac{4×0.2}{10}}=\frac{3\sqrt{2}}{5}m$.
(3)当小球到达最高点,刚好由重力提供向心力时,速度最小,根据牛顿第二定律得:
mg=m$\frac{{{v}_{min}}^{2}}{R}$
解得:${v}_{min}=\sqrt{gR}=\sqrt{2}m/s$.
答:(1)小球经过三个位置时对轨道的压力分别为27N、16N、7N;
(2)小球从C点飞出落到水平面上,其着地点与A点相距$\frac{3\sqrt{2}}{5}m$;
(3)小球在最高点不脱离轨道的最小速率为$\sqrt{2}m/s$.
点评 本题考查了圆周运动和平抛运动的综合运用,知道圆周运动向心力的来源,以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中物理 来源: 题型:选择题
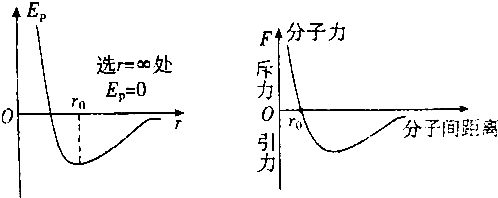
| A. | 分子力是零,分子势能也是零 | B. | 分子力是零,分子势能不是零 | ||
| C. | 分子力不是零,分子势能是零 | D. | 分子力不是零,分子势能不是零 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
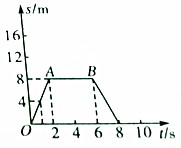 如图所示是质点在0~8s内的位移-时间图象,下列说法正确的是( )
如图所示是质点在0~8s内的位移-时间图象,下列说法正确的是( )| A. | 质点在第1s的位移为4m | |
| B. | 质点在第1s末的速度为4m/s | |
| C. | 点在2s~4s内做匀速直线运动 | |
| D. | 质点在前2s和最后2s的运动方向相反,但前2s速度更大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
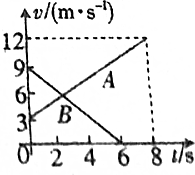 两个完全相同的物块A、B,在同一粗糙水平面上以不同的初速度从同一位置开始运动.图中两条直线分别表示物块受到水平拉力作用和不受拉力作用的v-t图象,求:
两个完全相同的物块A、B,在同一粗糙水平面上以不同的初速度从同一位置开始运动.图中两条直线分别表示物块受到水平拉力作用和不受拉力作用的v-t图象,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 体重计示数将变小 | |
| B. | 体重计示数将变大 | |
| C. | 体重计示数不变 | |
| D. | 如果力足够大,体重计和人会被一起提起 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
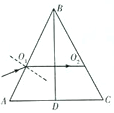 如图所示,一等边三棱镜ABC由两种材料组成,三棱镜ABD的折射率为n1,三棱镜CBD的折射率为n2,一束光照射到AB面上的O1点,其入射角为45°,该光的折射光线刚好与AC面平行,该光在O2点刚好发生全反射,三棱镜ABD的折射率为$\sqrt{2}$,该光在三棱镜CBD中传播的速率为$\frac{c}{2}$(已知光速为c).
如图所示,一等边三棱镜ABC由两种材料组成,三棱镜ABD的折射率为n1,三棱镜CBD的折射率为n2,一束光照射到AB面上的O1点,其入射角为45°,该光的折射光线刚好与AC面平行,该光在O2点刚好发生全反射,三棱镜ABD的折射率为$\sqrt{2}$,该光在三棱镜CBD中传播的速率为$\frac{c}{2}$(已知光速为c).查看答案和解析>>
科目:高中物理 来源: 题型:多选题
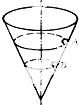 一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大(如图),则( )
一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大(如图),则( )| A. | 两球的向心力都等于重力和筒壁的支持力的合力 | |
| B. | A球的角速度大于B球的角速度 | |
| C. | A球的线速度大于B球的线速度 | |
| D. | A球的运动周期大于B球的运动周期 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
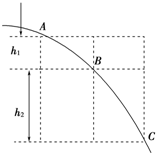 一个同学在“研究平抛物体运动”实验中,只画出了如图所示的一部分曲线,于是他在曲线上取水平距离△s相等的三点A、B、C,量得△s=0.2m.又量出它们之间的竖直距离分别为h1=0.1m,h2=0.2m,利用这些数据,可求得:
一个同学在“研究平抛物体运动”实验中,只画出了如图所示的一部分曲线,于是他在曲线上取水平距离△s相等的三点A、B、C,量得△s=0.2m.又量出它们之间的竖直距离分别为h1=0.1m,h2=0.2m,利用这些数据,可求得:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
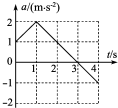 某同学在开展研究性学习的过程中,利用加速度传感器研究某一物体以初速度2m/s做直线运动的加速度a随时间t变化的规律,并在计算机上得到了前4s内物体加速度随时间变化的关系图象,如图所示.以物体的初速度方向为正方向.则下列说法正确的是( )
某同学在开展研究性学习的过程中,利用加速度传感器研究某一物体以初速度2m/s做直线运动的加速度a随时间t变化的规律,并在计算机上得到了前4s内物体加速度随时间变化的关系图象,如图所示.以物体的初速度方向为正方向.则下列说法正确的是( )| A. | 物体在1 s末速度方向改变 | |
| B. | 物体在3 s末速度方向改变 | |
| C. | 前4 s内物体的最大速度出现在第3 s末,大小为3.5 m/s | |
| D. | 物体在第2 s末与第4 s末的速度大小相等,方向也相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com