
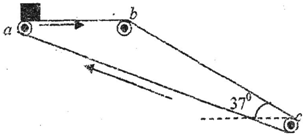
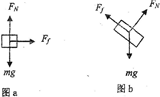
 解:(1)物块A放于传送带上后,物块受力图如答图a所示.
解:(1)物块A放于传送带上后,物块受力图如答图a所示.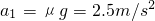
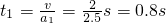
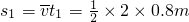 .
.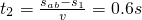
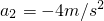 .
.

科目:高中物理 来源: 题型:单选题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
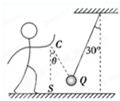 某同学表演魔术时,将一小型条形磁铁藏在自己的袖子里,然后对着一悬挂的金属小球指手画脚,结果小球在他神奇的功力下飘动起来.假设当隐藏的小磁铁位于小球的左上方某一位置C(∠QCS=30°)时,金属小球偏离竖直方向的夹角θ也是30°,如图所示.已知小球的质量为m,该同学(含磁铁)的质量为M,求此时:
某同学表演魔术时,将一小型条形磁铁藏在自己的袖子里,然后对着一悬挂的金属小球指手画脚,结果小球在他神奇的功力下飘动起来.假设当隐藏的小磁铁位于小球的左上方某一位置C(∠QCS=30°)时,金属小球偏离竖直方向的夹角θ也是30°,如图所示.已知小球的质量为m,该同学(含磁铁)的质量为M,求此时:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
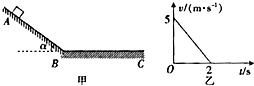 如图甲所示,斜面AB和水平面BC与滑块间的动摩擦因数相同,AB斜面的倾角α=37°.一质进为1kg的滑块从AU斜面上由静止开始下滑,不计滑块经过连接处B的能量损失,从 滑块滑上水平面BC开始计时,其运动的图象如图乙所示.重力加速度g取10m/s2,已知sin37°=0.6,cos37°=0.8.试求:
如图甲所示,斜面AB和水平面BC与滑块间的动摩擦因数相同,AB斜面的倾角α=37°.一质进为1kg的滑块从AU斜面上由静止开始下滑,不计滑块经过连接处B的能量损失,从 滑块滑上水平面BC开始计时,其运动的图象如图乙所示.重力加速度g取10m/s2,已知sin37°=0.6,cos37°=0.8.试求:查看答案和解析>>
科目:高中物理 来源: 题型:单选题
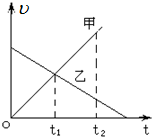 甲、乙两辆汽车从同一地点沿同一条平直的公路运动,它们的υ-t图象如图所示,由此可知
甲、乙两辆汽车从同一地点沿同一条平直的公路运动,它们的υ-t图象如图所示,由此可知查看答案和解析>>
科目:高中物理 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com