Question

如图3-6所示，排球场总长为18 m，设球网高度为2 m，运动员站在离网3 m的线上（图中虚线所示）正对网前跳起将球水平击出（空气阻力不计）．

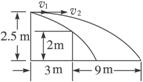
图3-6

（1）设击球点在3 m线正上方高度为2.5 m处，试问击球的速度在什么范围内才能使球既不触网也不越界．

（2）若击球点在3 m线正上方的高度小于某个值，那么无论水平击球的速度多大，球不是触网就是越界，试求这个高度（g取10 m／s²）．

Answer 1

解析：（1）作出如图3-7所示的平面图，若刚好不触网，设球的速度为v₁，则水平位移为3 m的过程中：

图3-7

水平方向有：s=v₀t，即3=v₁t                                                   ①

竖直方向有：y=，

即2.5-2=                                                               ②

由①②两式得：v₁= m/s

同理可得刚好不越界的速度

v₂=12 m/s

故速度范围为： m/s＜v＜12 m/s．

（2）设发球高度为H时，发出的球刚好越过球网落在边界线上，则刚好不触网时有：

s=v₀t，即3=v₀t                                                                  ③

H-h=，即H-2=                                                       ④

同理，当球落在界线上时有12=v₀t′                                                ⑤

H=                                                                      ⑥

解③④⑤⑥得H=2.13 m

即当击球高度小于2.13 m时，无论球的水平速度是多大，则球不是触网就是越界．

答案：（1） m/s＜v＜12 m/s  （2）2.13 m