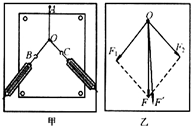
解:(1)①小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;
其次:设小车质量M,钩码质量m,整体的加速度为a,绳上的拉力为F,则:对小车有:F=Ma;对钩码有:mg-F=ma,即:mg=(M+m)a;
如果用钩码的重力表示小车受到的合外力,则要求:Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量,这样两者才能近似相等.
②C是BD的中间时刻,所以C点的速度就等于BD过程中的平均速度:
即:v
C=

=

验证合外力的功与动能变化间的关系只需验证:mgx=

Mv
2,所以需要测量的物理量有:钩码的重力和小车的总质量.
(2)图象如图所示:
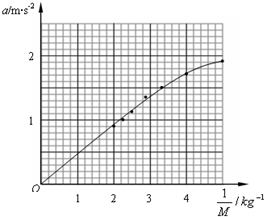
由图象可知,随着
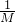
的增大,小车质量逐渐减小,不再满足小车质量远大于沙和砂桶的总质量,因此图象出现了偏折.
即原因是不再满足小车质量远大于沙和砂桶的总质量.
故答案为:(1)①a.平衡摩擦力
b.钩码的重力远小于小车的总重力
②

,钩码的重力和小车的总质量
(2)图象如图,
不再满足小车质量远大于沙和砂桶的总质量
分析:1、小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;其次:设小车加速度为a,则:绳上的力为F=Ma,对钩码来说:mg-Ma=ma,即:mg=(M+m)a,如果用钩码的重力表示小车受到的合外力,则Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量.
C是BD的中间时刻,所以C点的速度就等于BD过程中的平均速度.验证合外力的功与动能变化间的关系的原理:mgx=

Mv
2,根据等式得需要测量的物理量
2、描点法作图,根据“探究加速度与力、质量的关系”实验原理结合图象特点即可正确回答.
点评:要明确此题在验证合外力的功与动能变化间的关系中用到的原理,围绕原理,记忆需要测量的物理量及实验时的注意事项


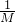 /kg-1
/kg-1 =
=
 Mv2,所以需要测量的物理量有:钩码的重力和小车的总质量.
Mv2,所以需要测量的物理量有:钩码的重力和小车的总质量.
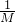 的增大,小车质量逐渐减小,不再满足小车质量远大于沙和砂桶的总质量,因此图象出现了偏折.
的增大,小车质量逐渐减小,不再满足小车质量远大于沙和砂桶的总质量,因此图象出现了偏折. ,钩码的重力和小车的总质量
,钩码的重力和小车的总质量 Mv2,根据等式得需要测量的物理量
Mv2,根据等式得需要测量的物理量

 星级口算天天练系列答案
星级口算天天练系列答案

 Ⅰ、在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某-点并记下该点的位置;再将橡皮条的另一端系两根细绳,细绳的另一端都有绳套,用两个弹簧秤分别勾住绳套,并互成角度地拉像皮条.
Ⅰ、在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某-点并记下该点的位置;再将橡皮条的另一端系两根细绳,细绳的另一端都有绳套,用两个弹簧秤分别勾住绳套,并互成角度地拉像皮条.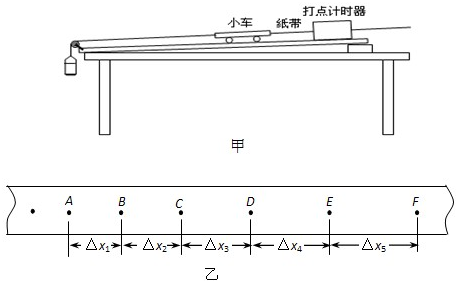
 在“探究恒力做功与动能改变的关系”实验中,为了提高测量的效率,现改用光电门来测量小车经过不同位置时的速度大小(光电门具有计时功能,与计算机相连后通过相关软件处理,可以直接读出物体的瞬时速度值),同学们在实验室组装了一套如图所示的装置.请回答下列有关问题:
在“探究恒力做功与动能改变的关系”实验中,为了提高测量的效率,现改用光电门来测量小车经过不同位置时的速度大小(光电门具有计时功能,与计算机相连后通过相关软件处理,可以直接读出物体的瞬时速度值),同学们在实验室组装了一套如图所示的装置.请回答下列有关问题:
