
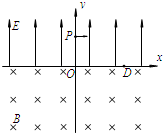
 ��2013?����һģ������ͼ��ʾ��xoy����ϵ�У�y��0�������ڴ�������y��������ǿΪE����ǿ�糡��y��0�������ڴ����Ŵ�ֱֽ������Ÿ�Ӧǿ��ΪB����ǿ�ų���һ�������Ӵ�y���ϵ�P��0��h��������x��������ij��ٶ������ǡ����ͨ��x���ϵ�D��d��0���㣮��֪�������ӵ�����Ϊm��������Ϊ-q��h��d��q������0������������Ӱ�죮
��2013?����һģ������ͼ��ʾ��xoy����ϵ�У�y��0�������ڴ�������y��������ǿΪE����ǿ�糡��y��0�������ڴ����Ŵ�ֱֽ������Ÿ�Ӧǿ��ΪB����ǿ�ų���һ�������Ӵ�y���ϵ�P��0��h��������x��������ij��ٶ������ǡ����ͨ��x���ϵ�D��d��0���㣮��֪�������ӵ�����Ϊm��������Ϊ-q��h��d��q������0������������Ӱ�죮
| 1 |
| 2 |
| qE |
| m |
|
| v2 |
| R |

|
| 2E |
| B |
| d |
| 2n+1 |
|
| n |
| 2n+1 |
| 2E |
| B |
|
|
| 2E |
| B |
| d |
| 2n+1 |
|
| n |
| 2n+1 |
| 2E |
| B |


 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�
 ��2013?����һģ���ҹ����Ҵ��Ժ�ⲿ�������Σ�������Ҵ��Ժ���ݶ�Ϊ�����Σ�һ������ԱΪִ������������ð���ڰ������ݶ����ϻ������У������������Ĺ����У�������
��2013?����һģ���ҹ����Ҵ��Ժ�ⲿ�������Σ�������Ҵ��Ժ���ݶ�Ϊ�����Σ�һ������ԱΪִ������������ð���ڰ������ݶ����ϻ������У������������Ĺ����У��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
| 1 |
| 6 |
| 1 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com