运动会上4×100m接力赛是最为激烈的比赛项目,有甲乙两运动员在训练交接棒的过程中发现,甲短距离加速后能保持9m/s的速度跑完全程.为了确定乙起跑的时机,甲在接力区前s0处作了标记,当甲跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时立即起跑(忽略声音传播的时间及人的反应时间),先做匀加速运动,速度达到最大后,保持这个速度跑完全程.已知接力区的长度为L=20m,试求:
(1)若s0=13.5m,且乙恰好在速度达到与甲相同时被甲追上,完成交接棒,则在完成交接棒时乙离接力区末端的距离为多大?
(2)若s0=16m,乙的最大速度为8m/s,要使甲乙能在接力区内完成交接棒,且比赛成绩最好,则乙在加速阶段的加速度应为多少?
解:(1)设经过时间t,甲追上乙,
根据题意有:vt-

=s
0,
将v=9m/s,s
0=13.5m代入得:t=3s,
此时乙离接力区末端的距离为△s=L-

=20-
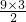
=6.5m
(2)因为甲、乙的最大速度:v
甲>v
乙,所以在完成交接棒时甲走过的距离越长,成绩越好.因此应当在接力区的末端完成交接,且乙达到最大速度v
乙.
设乙的加速度为a,加速的时间
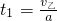
,在接力区的运动时间t=

,
∴L=

at
12+v
乙(t-t
1),解得:a=

m/s
2=2.67 m/s
2 答:(1)完成交接棒时乙离接力区末端的距离为6.5m.
(2)乙在加速阶段的加速度应为2.67 m/s
2.
分析:(1)甲追上乙时,位移之差等于s
0,根据匀变速直线运动的平均速度公式,抓住位移关系求出追及的时间,从而求出在完成交接棒时乙离接力区末端的距离.
(2)甲、乙的最大速度:v
甲>v
乙,所以在完成交接棒时甲走过的距离越长,成绩越好.因此应当在接力区的末端完成交接,且乙达到最大速度.通过乙先做匀加速直线运动,再做匀速直线运动,通过加速的时间和匀速的时间,求出匀加速直线运动的加速度.
点评:解决本题的关键理清运动过程,运用运动学公式灵活求解.

 =s0,
=s0, =20-
=20-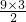 =6.5m
=6.5m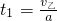 ,在接力区的运动时间t=
,在接力区的运动时间t= ,
, at12+v乙(t-t1),解得:a=
at12+v乙(t-t1),解得:a= m/s2=2.67 m/s2
m/s2=2.67 m/s2 
