
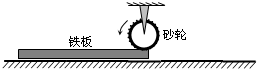
 如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.
如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.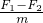 =1m/s2;
=1m/s2;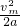 =2m<2.8m;
=2m<2.8m;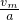 =
= s=2s;
s=2s;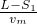 =
=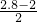 s=0.4s;
s=0.4s; mv2=
mv2= ×10×22J=20J;
×10×22J=20J;

科目:高中物理 来源: 题型:
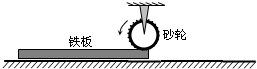 如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.
如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的砂轮下,工作时砂轮对铁板产生恒定的竖直向下的压力为100N,在砂轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,(g取10m/s2)
如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的砂轮下,工作时砂轮对铁板产生恒定的竖直向下的压力为100N,在砂轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
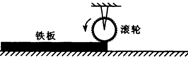 如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10kg.已知滚轮与铁板间的动摩擦因数为0.5,忽略铁板与工作台面间的摩擦.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.
如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10kg.已知滚轮与铁板间的动摩擦因数为0.5,忽略铁板与工作台面间的摩擦.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,用半径为0.4m的电动滚轮在长薄铁板的上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10.0kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放人工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板南静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5.0rad/s,g=10m/s2.
如图所示,用半径为0.4m的电动滚轮在长薄铁板的上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10.0kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放人工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板南静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5.0rad/s,g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:
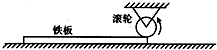 如图所示,用半径为0.4m的电动滚轮在薄铁板上表面压轧一道浅槽,铁板长L=2.8m,质量m=10Kg,已知滚轮与铁板,铁板与工作台面间的动摩擦因数分别为0.3和0.1,开始时把铁板的右端放入滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦力作用下铁板由静止开始向右运动并被压轧出一浅槽,已知滚轮转动的角速度恒为5rad/s,g取10m/s2,求:
如图所示,用半径为0.4m的电动滚轮在薄铁板上表面压轧一道浅槽,铁板长L=2.8m,质量m=10Kg,已知滚轮与铁板,铁板与工作台面间的动摩擦因数分别为0.3和0.1,开始时把铁板的右端放入滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦力作用下铁板由静止开始向右运动并被压轧出一浅槽,已知滚轮转动的角速度恒为5rad/s,g取10m/s2,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com